Метод наискорейшего спуска. Название метода можно было бы понимать буквально, если бы речь шла о минимизации функции цели

Название метода можно было бы понимать буквально, если бы речь шла о минимизации функции цели. Тем не менее по традиции такое название используется и при решении задачи на максимум. Метод в основном применяется для нахождения глобального экстремума в условиях отсутствия ограничений. Идея данного метода основана на том, что градиент функции указывает направление ее наиболее быстрого возрастания в окрестности той точки, в которой он вычислен. Поэтому, если из некоторой текущей точки 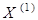перемещаться в направлении вектора 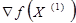, то функция f будет возрастать, по крайней мере, в некоторой окрестности 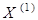. Следовательно, можно записать такую рекуррентную формулу

, (29)

где 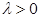- шаг итерации. Его выбор представляет самостоятельную задачу. Но достаточно часто его назначают в пределах 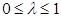и затем уточняют.

Метод реализуется по следующей схеме:

1) задают первоначальную точку отсчета (для успешного решения задачи

начальная точка должна быть максимально приближена к предполагае-

мому экстремуму);

2) находят частные производные функционала (значения частных

производных в начальной точке);

3) находят значение функции в начальной точке;

4) по параметрам начальной точки вычисляют градиент функции;

5) по формуле (29) находят параметры новой точки;

6) если удовлетворяются условия уравнения 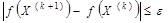, то

процесс прекращают, в противном случае возвращаются к пункту 2.

З а д а ч а 28. Найти максимальное значение функции

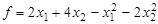
при точности вычислений .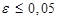

Р е ш е н и е. Найдем градиент функции:

;

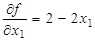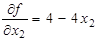
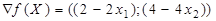
Возьмем в качестве первого приближения 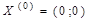, т.е. 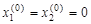. Тогда значение функции 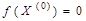, а вектор-строка градиента функции равен . Выберем шаг итерации 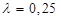и рассчитаем параметры следующей точки:

,

.

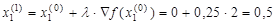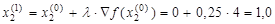Вычислим значение функции цели в новой точке и определим степень приближения:

.

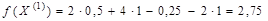
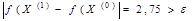Так как заданная точность не достигнута, продолжим итерационный процесс. Градиент функции в новой точке будет определяться вектор-строкой 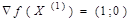. Рассчитаем параметры следующей точки:

,

.

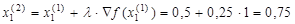Значение функции цели в исследуемой точке и степень приближения равны:

,

.

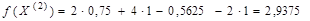Продолжим вычисления. В точке 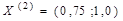градиент функции будет иметь следующий вектор-строку: 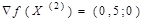. Рассчитываем параметры третьей точки итерации:

,

.

Функция цели в третьей точке примет значение

.

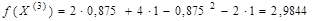Соответственно полученная точность:

.

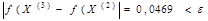Тогда в пределах заданной точности ответ следующий:

, .

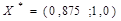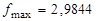Если точность недостаточна, процесс итерации следует продолжить. Теоретическое решение данной задачи: , .

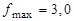В градиентных методах успех решения и достигаемая точность существенно зависит от двух основных факторов:

- параметров начальной точки движения (она должна быть максимально приближена к предполагаемому экстремуму);

- величины множителя λ.

Если нарушается требование по начальной точке движения, то в этом случае метод может увести процесс итерации от ожидаемого экстремума и задача вообще не будет решена. Если же наблюдается несоответствие по второму требованию, т.е. λ будет слишком велико, то задача также может не иметь решения, так как зона нахождения экстремума «не замечается». Однако стремление иметь λ как можно меньше существенно увеличивает объем расчетного процесса.

Поиск по сайту: