Средние значения и стандартные ошибки исследований

Средние величины в статистическом понимании — это обоб­щающие показатели совокупности однотипных явлений по ка­кому-либо количественному признаку. Целью определения сред­них величин является:

• ослабить влияние случайных факторов на изучаемый по­казатель;

• получить сводный показатель, описывающий данную со­вокупность в целом.

Средние величины разделяются на математические и струк­турные. К математическим относят среднеарифметические, сред­негеометрические и гармонические, к структурным — моду и медиану.

Среднеарифметическая простая равна простой сумме значений осредняемого признака, деленной на общее число этих зна­чений.

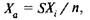
где n-число единиц совокупности.

Среднеарифметическая взвешенная исчисляется для сгруппи­рованных данных следующим образом:

где Х_a - варианты значений признака;

Средняя геометрическая:

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой отно­сительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уров­ня в ряду динамики, т.е. средняя геометрическая характеризует средний коэффициент роста. Этот показатель используется при расчете индексов, определении средних темпов изменения в рядах динамики, а также в рядах распределения.

Средняя гармоническая величина обратная средней арифмети­ческой из обратных значений признака. Средняя гармоническая применяется в тех случаях, когда известны варианты признака, его объемное значение, но не известны частоты;

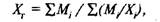
где M_i — объемное значение признака;

X _i— его варианты.

Мода— наиболее типичное, чаще всего встречаемое значение признака. В случаях интервальных рядов с равными интервала­ми модальным интервалом считается интервал с наибольшей частотой, а при неравных интервалах — интервал с наибольшей плотностью.

Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация изучаемого признака скры­вается за средними. Основа показателей общая — оценка откло­нений значений показателей элементов совокупности от сред­ней.

Размах представляет собой разность между максимальной и минимальной величиной признака:

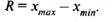
Среднее линейное отклонение:

где х, —значение показателя;

X— среднее арифметическое значение. Среднее линейное отклонение в «чистом» виде для анализа не применя­ют, используя как составляющую для вычисления среднего относительного отклонения:

Сумма квадратов отклонений является основой для вычисления относительного показателя — дисперсии:

или для интервальных рядов: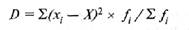

Среднее квадратическое отклонение:

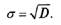
Среднеквадратическое отклонение показывает, как располо­жена основная масса единиц совокупности относительно среднеарифметической.

Для получения представления о форме распределения случай­ной величины строят графики распределения (полигон и гистог­рамму). Кривая распределения характеризует теоретическое рас­пределение, которое получилось бы при полном погашении всех случайных причин. Исследование закономерности включает ре­шение трех задач: 1) выяснение общего характера распределения; 2) построение кривой на эмпирическом распределении; 3) про­верка соответствия эмпирического распределения теоретической кривой.

Поиск по сайту: