 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПОЛИТИЧЕСКАЯ
 теңдеуін кесінділік түрге келтіріңіз
теңдеуін кесінділік түрге келтіріңіз
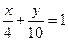
 шеңберінің центрінің координатасын табыңыз
шеңберінің центрінің координатасын табыңыз
(1, 0)
 және
және  нүктелері арқылы өтетін түзудің теңдеуін жазыңыз
нүктелері арқылы өтетін түзудің теңдеуін жазыңыз
A) 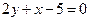
 түзуінің теңдеуін кесінділік теңдеу түрінде жазыңыз
түзуінің теңдеуін кесінділік теңдеу түрінде жазыңыз
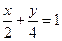
 нүктесі арқылы және
нүктесі арқылы және  векторына перпендикуляр өтетін түзудің теңдеуін жазыңыз
векторына перпендикуляр өтетін түзудің теңдеуін жазыңыз
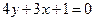
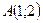 нүктесінен
нүктесінен 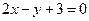 түзуіне дейінгі арақашықтықты табыңыз
түзуіне дейінгі арақашықтықты табыңыз
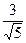
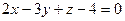 жазықтығының теңдеуін кесінділік теңдеу түрінде жазыңыз
жазықтығының теңдеуін кесінділік теңдеу түрінде жазыңыз
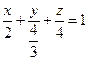
 нүктесі арқылы
нүктесі арқылы  векторына перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз
векторына перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз
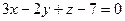
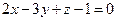 және
және  жазықтықтарының арасындағы бұрыштың косинусын табыңыз
жазықтықтарының арасындағы бұрыштың косинусын табыңыз
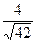
Бұрыштық коэффициенті  және
және 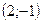 нүктесі арқылы өтетін түзудің теңдеуін жазыңыз
нүктесі арқылы өтетін түзудің теңдеуін жазыңыз
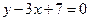
 нүктесінен
нүктесінен  жазықтығына дейінгі арақашықтықты табыңыз
жазықтығына дейінгі арақашықтықты табыңыз
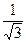
 нүктесі арқылы және
нүктесі арқылы және  векторына параллель өтетін түзудің теңдеуін жазыңыз
векторына параллель өтетін түзудің теңдеуін жазыңыз
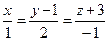
 және
және 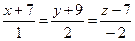 түзулерінің арасындағы бұрыштың косинусын табыңыз
түзулерінің арасындағы бұрыштың косинусын табыңыз
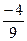
 және
және  жазықтықтары
жазықтықтары 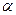 мен
мен  -ның қандай мәндерінде өзара параллель болады?
-ның қандай мәндерінде өзара параллель болады?
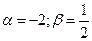
 және
және  нүктелері арқылы өтетін түзудің теңдеуін жазыңыз
нүктелері арқылы өтетін түзудің теңдеуін жазыңыз
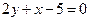
 және
және  түзулерінің арасындағы сүйір бұрышты табыңыз
түзулерінің арасындағы сүйір бұрышты табыңыз
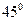
 түзуінің теңдеуін кесінділік теңдеу түрінде жазыңыз
түзуінің теңдеуін кесінділік теңдеу түрінде жазыңыз
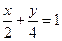
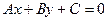 теңдеуінде
теңдеуінде  болса, онда түзу қалай орналасқан?
болса, онда түзу қалай орналасқан?
координаттардың бас нүктесі арқылы өтеді
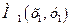 және
және 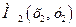 нүктелерінің ара қашықтығын есептейтін формуланы көрсетіңі з
нүктелерінің ара қашықтығын есептейтін формуланы көрсетіңі з
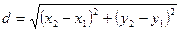
 және
және  нүктелерінің ара қашықтығын табыңыз
нүктелерінің ара қашықтығын табыңыз
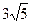
 шеңберінің радиусын анықтаңыз
шеңберінің радиусын анықтаңыз
3 
 параболасының төбесінің координаталарын табыңыз
параболасының төбесінің координаталарын табыңыз
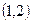
Мына түзулердің қайсысы 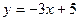 түзуіне параллель?
түзуіне параллель?
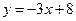
Центрі координат бас нүктесімен беттесетін, диаметрі 6-ға тең шеңбердің теңдеуін құрыңыз


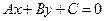 түзуінде
түзуінде  болса, онда түзу...
болса, онда түзу...
Ох өсіне параллель
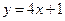 және
және 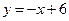 түзулерінің қиылысу нүктелерінің координаталарын табыңыз
түзулерінің қиылысу нүктелерінің координаталарын табыңыз
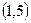
 және
және  түзулерінің арасындағы бұрышты табыңыздар
түзулерінің арасындағы бұрышты табыңыздар


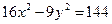 гиперболасының фокустарының арақашықтығын табыңыздар
гиперболасының фокустарының арақашықтығын табыңыздар
 нүктесі арқылы
нүктесі арқылы  түзуіне параллель өтетін түзудің теңдеуін жазыңыз
түзуіне параллель өтетін түзудің теңдеуін жазыңыз
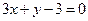
 параболасының р параметрін табыңыз
параболасының р параметрін табыңыз
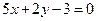 түзуіне перпендикуляр түзудің бұрыштық коэффициентін табыңыз
түзуіне перпендикуляр түзудің бұрыштық коэффициентін табыңыз
2/5
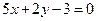 түзуіне параллель түзудің бұрыштық коэффициентін табыңыз
түзуіне параллель түзудің бұрыштық коэффициентін табыңыз
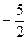
 және
және  түзулерінің қиылысу нүктелерінің координаталарын табыңыз
түзулерінің қиылысу нүктелерінің координаталарын табыңыз
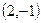
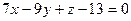 жазықтығының нормаль векторын көрсетіңіз
жазықтығының нормаль векторын көрсетіңіз
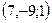
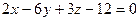 жазықтығының нормаль векторын көрсетіңіз
жазықтығының нормаль векторын көрсетіңіз
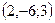
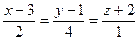 түзуінің бағыттаушы векторын көрсетіңіз
түзуінің бағыттаушы векторын көрсетіңіз 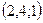
 түзуінің бағыттаушы векторын көрсетіңіз
түзуінің бағыттаушы векторын көрсетіңіз
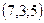
Мына теңдеулердің қайсысы эллипстің теңдеуі:
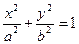
Мына теңдеулердің қайсысы гиперболаның теңдеуі:
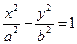
Мына теңдеулердің қайсысы параболаның теңдеуі:
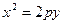
Мына теңдеулердің қайсысы шеңбердің теңдеуі:
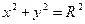
Екі  және
және  түзулерінің арасындағы бұрыш келесі формуламен есептелінеді:
түзулерінің арасындағы бұрыш келесі формуламен есептелінеді:
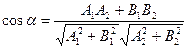
Екі  және
және 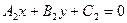 түзулерінің параллельдік белгісін көрсет
түзулерінің параллельдік белгісін көрсет
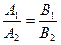
Екі  және
және 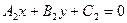 түзулерінің перпендикулярлық белгісін көрсет
түзулерінің перпендикулярлық белгісін көрсет
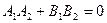
 эллипсінің жарты өстерін табыңыз
эллипсінің жарты өстерін табыңыз
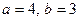
 нүктесі арқылы
нүктесі арқылы 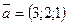 векторына параллель өтетін түзудің канондық теңдеуін жазыңыз
векторына параллель өтетін түзудің канондық теңдеуін жазыңыз
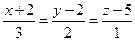
 нүктесі арқылы,
нүктесі арқылы,  түзуіне перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз
түзуіне перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз
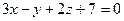
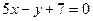 және
және  түзулерінің арасындағы бұрышты табыңыз
түзулерінің арасындағы бұрышты табыңыз
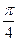
 нүктесі арқылы
нүктесі арқылы  векторына перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз
векторына перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз

 және
және  түзулерінің қиылысу нүктесін табыңыз
түзулерінің қиылысу нүктесін табыңыз
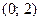
 шеңберінің центрінің координаттары мен радиусын табыңыз
шеңберінің центрінің координаттары мен радиусын табыңыз
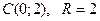
Бірінші тамаша шекті көрсетіңіз:
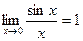
Екінші тамаша шекті көрсетіңіз:
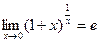
Екінші тамаша шекті көрсетіңіз:
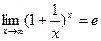

 функциялары берілсін.
функциялары берілсін. 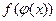 күрделі функциясын құраңыз:
күрделі функциясын құраңыз:
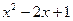
Шекті есептеңіз: 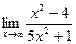
1/5
Шекті есептеңіз: 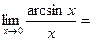
ті есептеңіз: 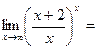
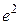
Лопиталь ережесін пайдаланып шекті есептеңіз: 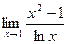
Шекті есептеңіз: 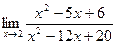
1/8
Шекті есептеңіз: 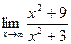
Шекті есептеңіз: 
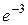
Шекті есептеңіз: 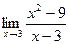
Шекті есептеңіз: 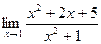
Шекті есептеңіз: 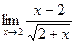
Шекті есептеңіз: 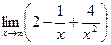
Шекті есептеңіз: 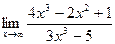
4/3
Шекті есептеңіз: 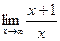
Шекті есептеңіз: 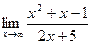
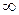
Шекті есептеңіз: 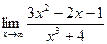
Шекті есептеңіз: 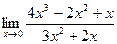
1/2
Шекті есептеңіз: 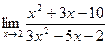
Шекті есептеңіз: 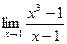
Шекті есептеңіз: 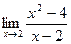
Шекті есептеңіз: 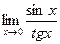
Шекті есептеңіз: 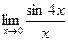
Шекті есептеңіз: 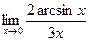
2/3
Шекті есептеңіз: 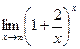
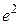 Шекті есептеңіз:
Шекті есептеңіз: 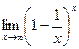
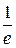
Шекті есептеңіз: 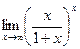
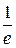
Шекті есептеңіз: 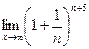
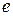
Шекті есептеңіз: 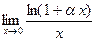
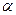
 функциясы берілген.
функциясы берілген. 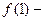 мәнін табыңыз:
мәнін табыңыз:
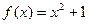 функциясы берілген.
функциясы берілген. 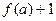 мәнін табыңыз:
мәнін табыңыз:
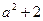
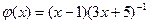 функциясы берілген.
функциясы берілген. 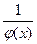 функциясын көрсетіңіз:
функциясын көрсетіңіз:
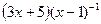
 функциясы берілген.
функциясы берілген.  мәнін табыңыз:
мәнін табыңыз:
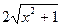

 функциялары берілген.
функциялары берілген.  мәнін табыңы з:
мәнін табыңы з:
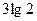
 функцияның анықталу облысын көрсетіңіз:
функцияның анықталу облысын көрсетіңіз:
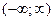
 функциясының анықталу облысын көрсетіңіз:
функциясының анықталу облысын көрсетіңіз:
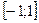
 функцияның анықталу облысын көрсетіңіз:
функцияның анықталу облысын көрсетіңіз:
 нүктесін көрсетіңіз:
нүктесін көрсетіңіз:
A) 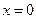 ;
; 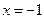
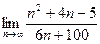 есептеңіз
есептеңіз
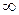
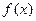 функцияның
функцияның 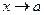 ұмтылғандағы шегі
ұмтылғандағы шегі  ға тең өрнекті көрсетіңіз:
ға тең өрнекті көрсетіңіз:
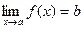
Шекті есептеңіз: 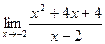
Шекті есептеңіз: 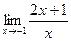
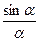 функцияның
функцияның  -дағы шегі:
-дағы шегі:
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 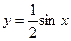 функциялары берілсін. Тақ функцияларды көрсетіңіз:
функциялары берілсін. Тақ функцияларды көрсетіңіз:
3 және 4
Егер  шектері бар, бірақ
шектері бар, бірақ 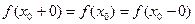 теңдіктерінің ең болмағанда біреуі орындалмаса, онда
теңдіктерінің ең болмағанда біреуі орындалмаса, онда 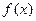 функциясы
функциясы  нүктесінде
нүктесінде
A) үзіледі.
Шекті есептеңіз: 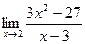
A) 15
 шексіз аз болғанда эквиваленттік шаманы көрсетіңіз:
шексіз аз болғанда эквиваленттік шаманы көрсетіңіз:
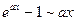
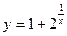 функциясының үзіліс нүктесін табыңыз:
функциясының үзіліс нүктесін табыңыз:
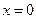
Шекті есептеңіз: 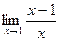 2
2
Шекті есептеңіз: 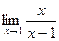
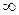
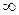 Төмендегі теңдіктердің қайсысы
Төмендегі теңдіктердің қайсысы 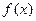 функциясының қандай да бір
функциясының қандай да бір  нүктесіндегі үзіліссіздікті көрсетеді?
нүктесіндегі үзіліссіздікті көрсетеді?
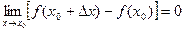
 функцияның үзіліс нүктесін және оның типін анықтаңыз:
функцияның үзіліс нүктесін және оның типін анықтаңыз:
 -II текті үзіліс
-II текті үзіліс
 функциясының үзілісіз нүктесін және осы нүктедегі сол жақ шегінің мәнін табыңыз:
функциясының үзілісіз нүктесін және осы нүктедегі сол жақ шегінің мәнін табыңыз:
 шегі
шегі 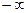
функциясының үзіліс нүктесін және осы нүктедегі оң жақ шегінің мәнін табыңыз:
2; шегі 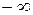
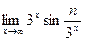 табыңыз
табыңыз
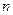
 да
да 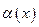 шексіз аз болса, онда эквиваленттік шамаларды көрсетіңіз.
шексіз аз болса, онда эквиваленттік шамаларды көрсетіңіз.
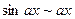 ,
, 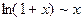
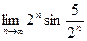 табыңыз
табыңыз
 табыңыз:
табыңыз:
3/4
 табыңыз:
табыңыз:
7/4
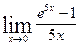 табыңыз:
табыңыз:
 функциясының анықталу облысын табыңыз:
функциясының анықталу облысын табыңыз:
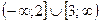
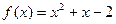 функциясы берілсін.
функциясы берілсін. 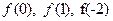 мәндерін табыңыз:
мәндерін табыңыз:
A) -2; 0; 0
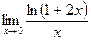 есептеу керек
есептеу керек
 есептеу керек
есептеу керек
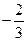
1)  , 2)
, 2) 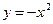 , 3)
, 3)  функцияларының қайсысы шектелген фу
функцияларының қайсысы шектелген фу
1 ) 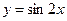 , 2)
, 2)  , 3)
, 3)  функцияларының қайсысы шектелмеген функция болады?
функцияларының қайсысы шектелмеген функция болады?
A) 3
1 ) 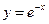 , 2)
, 2)  , 3)
, 3) 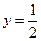 функцияларының қайсысы
функцияларының қайсысы 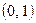 аралығында өседі?
аралығында өседі?
А) 2
1 )  , 2)
, 2)  , 3)
, 3)  функцияларының қайсысы
функцияларының қайсысы 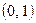 аралығында кемиді?
аралығында кемиді?
А) 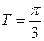
1)  , 2)
, 2) 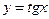 , 3)
, 3) 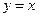 функцияларының қайсысы
функцияларының қайсысы  аралығында тұрақты болады?
аралығында тұрақты болады?
Шекті есептеңіз: 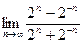
Шекті есептеңіз: 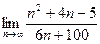
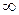
Шекті есептеңіз: 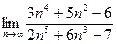
Шекті есептеңіз: 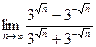
Шекті есептеңіз: 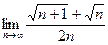
Шекті есептеңіз: 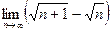
Шекті есептеңіз: 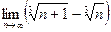
Шекті есептеңіз: 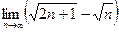
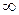
Шекті есептеңіз: 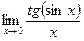
Шекті есептеңіз: 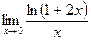
Шекті есептеңіз: 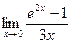
2/3
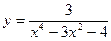 функциясының үзіліс нүктесін табыңыз:
функциясының үзіліс нүктесін табыңыз:
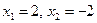
 функциясының үзіліс нүктесін табыңыз:
функциясының үзіліс нүктесін табыңыз:
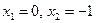
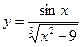 функциясының үзіліс нүктесін табыңыз:
функциясының үзіліс нүктесін табыңыз:
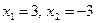
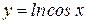 функциясының анықталу облысын табыңыз:
функциясының анықталу облысын табыңыз:
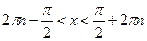
 функциясының мендер облысын табыңыз:
функциясының мендер облысын табыңыз:
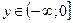
 функциясының периодын табыңыз:
функциясының периодын табыңыз:
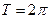
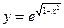 функциясының анықталу облысын табыңыз:
функциясының анықталу облысын табыңыз:
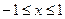
 функциясының мәндер облысын табыңыз:
функциясының мәндер облысын табыңыз:
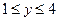
 функциясының периодын табыңыз:
функциясының периодын табыңыз:
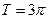
 функциясының периодын табыңыз:
функциясының периодын табыңыз:
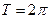
 функциясының периодын табыңыз:
функциясының периодын табыңыз:
Шекті есептеңіз: 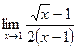
1/4
Шекті есептеңіз: 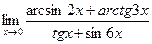
5/7
Шекті есептеңіз: 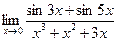
Шекті есептеңіз: 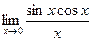
Шекті есептеңіз: 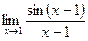
Шекті есептеңіз: 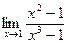
2/3
Шекті есептеңіз: 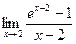
 функциясының
функциясының  нүктесiнде туындысы деп нені айтады?
нүктесiнде туындысы деп нені айтады?
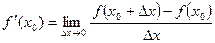
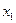 нүктесi
нүктесi 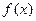 функциясының минимум нүктесi деп аталады, егер
функциясының минимум нүктесi деп аталады, егер  нүктесiнiң маңайында қандай теңсiздiк орындалатын болса?
нүктесiнiң маңайында қандай теңсiздiк орындалатын болса?
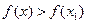
 функциясының
функциясының  нүктесiнде экстремумы болуы үшiн оның осы нүктедегi туындысы неге тең болады?
нүктесiнде экстремумы болуы үшiн оның осы нүктедегi туындысы неге тең болады?
нөлге тең  немесе болмайды
немесе болмайды
Егер екi рет дифференциалданатын 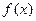 функциясының 1-шi ретті туындысы
функциясының 1-шi ретті туындысы  нүктесiнде 0-ге тең, ал екiншi туындысы
нүктесiнде 0-ге тең, ал екiншi туындысы 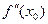 осы нүктеде оң болса, онда ол қандай нүкте болады?
осы нүктеде оң болса, онда ол қандай нүкте болады?
 минимум нүктесi
минимум нүктесi
Егер екi рет дифференциалданатын 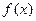 функциясының 1-шi ретті туындысы
функциясының 1-шi ретті туындысы  нүктесiнде 0-ге тең, ал 2-шi туындысы
нүктесiнде 0-ге тең, ал 2-шi туындысы 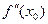 осы нүктеде терiс болса, онда онда ол қандай нүкте болады?
осы нүктеде терiс болса, онда онда ол қандай нүкте болады?
 – максимум нүктесi
– максимум нүктесi
Екi рет дифференциалданатын 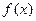 функциясының 2-шi ретті туындысының иiлу нүктесiндегi мәнi неге тең?
функциясының 2-шi ретті туындысының иiлу нүктесiндегi мәнi неге тең?
0-ге тең
Екi рет дифференциалданатын 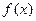 функциясының 2-шi ретті туындысы
функциясының 2-шi ретті туындысы  нүктесiнің маңайында таңбасын өзгеретiн болса, онда
нүктесiнің маңайында таңбасын өзгеретiн болса, онда  - қандай нүкте болады?
- қандай нүкте болады?
функцияның иiлу нүктесi
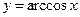 функциясының туындысын көрсетіңіз:
функциясының туындысын көрсетіңіз:
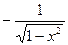
 функциясының туындысын көрсетіңіз:
функциясының туындысын көрсетіңіз:
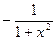
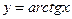 функциясының туындысының формуласын көрсетіңіз:
функциясының туындысының формуласын көрсетіңіз:
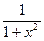
 функциясының туындысының формуласын көрсетіңіз:
функциясының туындысының формуласын көрсетіңіз:
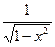
 функциясының туындысы неге тең?
функциясының туындысы неге тең?
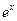
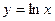 функциясының туындысы неге тең?
функциясының туындысы неге тең?
1/x
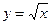 функциясының туындысы неге тең?
функциясының туындысы неге тең?
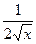
 туындысы, мұнда с-тұрақты
туындысы, мұнда с-тұрақты
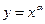 туындысы неге тең?
туындысы неге тең?
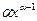
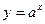 туындысы неге тең?
туындысы неге тең?
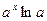
 туындысы неге тең?
туындысы неге тең? 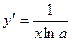
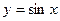 туындысы неге тең?
туындысы неге тең?
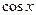
 туындысы неге тең?
туындысы неге тең?
A 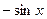
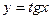 туындысы неге тең?
туындысы неге тең?
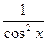
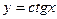 туындысы неге тең?
туындысы неге тең?
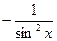
 нүктесі
нүктесі  функциясының максимум нүктесі деп аталады, егер
функциясының максимум нүктесі деп аталады, егер  нүктесінің маңайында қандай теңсіздік орындалады?
нүктесінің маңайында қандай теңсіздік орындалады?
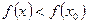
 функциясы туындысының
функциясы туындысының  нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
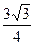
 функциясының туындысының
функциясының туындысының  нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
-1
 функциясының туындысының
функциясының туындысының 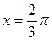 нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
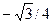
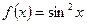 функциясының туындысының
функциясының туындысының 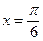 нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
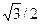
 функциясының туындысының
функциясының туындысының 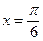 нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
-3
 функциясы туындысының
функциясы туындысының 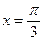 нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
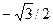
Функцияны экстремумға зерттеңіз: 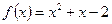
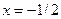 -минимум нүкте
-минимум нүкте
Функцияны экстремумға зерттеңіз: 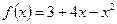
 -максимум нүкте
-максимум нүкте
Функцияны экстремумға зерттеңіз: 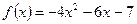
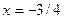 -максимум нүкте
-максимум нүкте
Функцияның туындысын табыңыз: 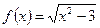
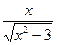
Функцияның туындысын табыңыз: 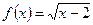
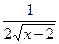
Функцияның туындысын табыңыз: 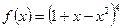
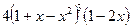
Функцияның туындысын табыңыз: 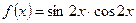
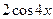
Функцияның туындысын табыңыз: 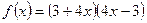
32х
Функцияның туындысын табыңыз: 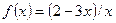
-2/х2
Функцияның туындысын табыңыз: 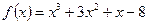
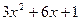
Функцияның туындысын табыңыз: 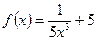
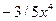
 функциясының бірінші ретті туындысының
функциясының бірінші ретті туындысының  -дегі мәнін табыңыз
-дегі мәнін табыңыз
0,5
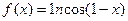 функциясының туындысын табыңыз
функциясының туындысын табыңыз
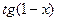
Функцияның туындысын табыңыз: 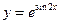
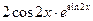
Функцияны экстремумға зерттеңіз: 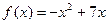
 максимум нүктесі
максимум нүктесі
 функциясы туындысының
функциясы туындысының  нүктесіндегі мәнін табыңыз
нүктесіндегі мәнін табыңыз
Егер  функциясы
функциясы  интервалында өспелі болса, онда бірінші туындысы қандай болады?
интервалында өспелі болса, онда бірінші туындысы қандай болады?
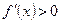
Егер  функциясы
функциясы  интервалында кемімелі болса, онда бірінші туындысы қандай болады?
интервалында кемімелі болса, онда бірінші туындысы қандай болады?
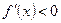
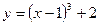 функциясының иілу нүктесін табыңыз:
функциясының иілу нүктесін табыңыз:
(1; 2)
 функциясының иілу нүктесін табыңыз:
функциясының иілу нүктесін табыңыз:
(0; 0)
 функциясының кему аралығын табыңыз:
функциясының кему аралығын табыңыз:
(-∞; 0)
Функциясының туындысын табу дегеніміз не?
дифференциалдау
 функциясының
функциясының 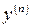 табыңыз:
табыңыз:
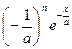
 функциясының туындысын тауып,
функциясының туындысын тауып, 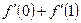 өрнегінің мәнін есептеңіз
өрнегінің мәнін есептеңіз
Функцияның туындысын табыңыз: 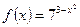
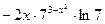
Функцияның туындысын табыңыз: 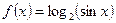
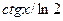
Функцияны экстремумға зерттеңіз: 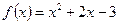
 , минимум нүктесі
, минимум нүктесі
Функцияның туындысын табыңыз: 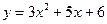
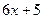
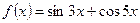 функцияның туындысын табыңыз:
функцияның туындысын табыңыз:
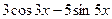
 функцияның туындысының
функцияның туындысының  мәнін есептеңіз:
мәнін есептеңіз:
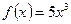 функциясының
функциясының 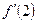 есептеңіз:
есептеңіз:
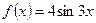 функциясының
функциясының 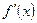 есептеңіз:
есептеңіз:
12cos3x
 функциясының
функциясының 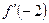 есептеңіз:
есептеңіз:
1,002
Туындыны табыңыз: 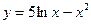
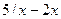
 функциясының
функциясының 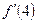 мәнін табыңыз:
мәнін табыңыз:
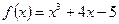 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
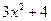
 функциясының туындысы
функциясының туындысы  -ті табыңыз:
-ті табыңыз:
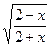
 функциясының
функциясының  табыңыз:
табыңыз:
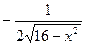
 функциясының
функциясының 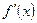 табыңыз:
табыңыз:
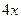
 функциясының
функциясының 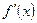 табыңыз:
табыңыз:
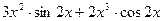
 функциясының
функциясының 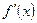 табыңыз:
табыңыз:
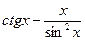
 функциясының
функциясының 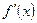 табыңыз:
табыңыз:
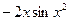
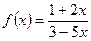 функциясының
функциясының 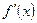 табыңыз:
табыңыз:
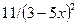
 функциясының
функциясының 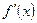 табыңыз:
табыңыз:
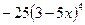
 функциясының
функциясының  табыңыз:
табыңыз:
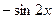
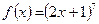 функциясының
функциясының  табыңыз:
табыңыз:
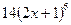
 функциясының
функциясының  табыңыз:
табыңыз:
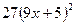
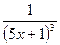 функциясының
функциясының  табыңыз:
табыңыз:
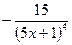
 функциясының
функциясының  табыңыз:
табыңыз:
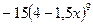
Поиск по сайту: