 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример. Продано, шт. Цена за единицу, т.руб. Товары в базисном периоде (q0) в отчетном периоде (q1) в базисном периоде (p0)
|
Читайте также: |
| Продано, шт. | Цена за единицу, т.руб. | |||
| Товары | в базисном периоде (q0) | в отчетном периоде (q1) | в базисном периоде (p0) | в отчетном периоде (p1) |
| А | 10 | 9 | 200 | 250 |
| Б | 20 | 22 | 300 | 280 |
| В | 30 | 25 | 50 | 100 |
Вычисляем: Ipq = 1,148; Iq = 1,016; Ip = 1,13.
Следовательно, выручка фирмы от продажи товаров А, Б, В в отчетном периоде увеличилась по сравнению с базисным периодом на 14,8 %. Однако, фактически продано этих товаров больше лишь на 1,6 %, цены на этот же период возросли на 13 %.
При анализе рынка часто бывают, необходимы сведения об изменении средней цены продажи товаров. В этом случае рассчитывают индекс средней цены (индекс переменного состава):
,
т.е. средние цены реализации увеличились по сравнению с базисным периодом на 23 % (по товару А они возросли на 25 %, по товару Б снизились на 7 %, а товару В увеличились в два раза).
3.3.4 Корреляционный анализ
Этот анализ позволяет установить наличие связи между двумя рассматриваемыми показателями (признаками). При этом вычисляются коэффициенты корреляции или корреляционные отношения.
Коэффициенты корреляции рассчитываются по формуле
,
где x – показатель факторного (причинного) признака;
y – показатель функционального (результативного) признака;
n – число взаимосвязанных пар этих показателей.
Корреляционное отношение вычисляется по формуле:
,
где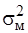 
- дисперсия межгрупповая;
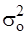- дисперсия общая.
Коэффициент корреляции изменяется от – 1 до + 1. Чем его значение ближе к 1, тем связь между факторами и результатами теснее.
В маркетинговых исследованиях результат анализа считается достаточно надежным, если rxy ³ 0,5.
Пример. Установить наличие связи путем вычисления коэффициента корреляции между доходами хозяйств и приобретением ими техники.
| Доходы, у.е. | Приобретение техники, шт (Y) | Середина доходного интервала (X) | XY | Y2 | X2 |
| До 8 | 5 | 4 | 20 | 25 | 16 |
| 9-16 | 5,5 | 12 | 66 | 30,25 | 144 |
| 17-19 | 6,5 | 18 | 117 | 42,25 | 324 |
| 20-30 | 6,9 | 25 | 172,5 | 47,61 | 625 |
| 31-40 | 7 | 35 | 245 | 49 | 1225 |
| 41-50 | 8,5 | 45 | 382,5 | 72,25 | 2025 |
| Выше 50 | 10 | 55 | 550 | 100 | 3025 |
| Всего | 49.4 | 194 | 1553 | 366,36 | 7384 |
В результате расчета получаем, т.е. rxy
.
Если показатель факторного признака не может быть выражен в количественной форме, то вычисляют коэффициент корреляции рангов:
,
где Rx – ранг признака X;
Ry - ранг признака Y;
n – число взаимосвязанных пар показателей.
Это имеет место, если устанавливается зависимость потребления сельхозтехники от вида собственности хозяйства.
Поиск по сайту: