 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример
|
Читайте также: |
| Вид | Потребление | Ранги (R) | Разность между | ||
| собственности | техники, шт | по видам собственности | по потреблению | рангами (d) | d2 |
| Акционерное | 4,2 | 3 | 2,5 | 0,5 | 0,25 |
| Фермерское | 4 | 2 | 1,5 | 0,5 | 0,25 |
| Коллективное | 3,8 | 1 | 1 | 0 | 0 |
| Итого | 0,5 |
.
Величина рангового коэффициента корреляции близка к 1, т.е. связь между формой собственности хозяйства и приобретением техники достаточно надежная, а риск маркетинговых решений, принимаемых на основе анализа этой зависимости небольшой.
3.3.5 Регрессионный анализ
Регрессионный анализ представляет собой подбор математических зависимостей, описывающих исследуемые связи. Элементы рынка зависят от различных факторов, и формы этих зависимостей могут быть самыми разнообразными. Поэтому регрессионный анализ начинают с построения графика, а за тем подбирают наиболее отвечающую математическую зависимость.
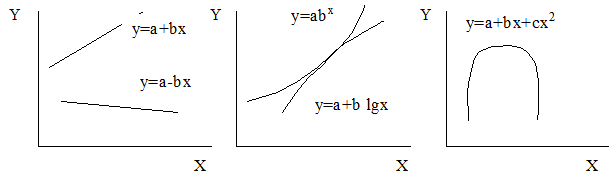Рисунок 3.7 – Графики зависимости элементов рынка
от формирующих факторов
Таблица - Простейшие виды уравнений регрессии и системы уравнений для определения их параметров
| Форма зависимости | Уравнение регрессии | Системы нормальных уравнений |
| 1. Прямая | y = a + bx | 
|
| 2. Полулогарифмичесая | y = a + b lgx | 
|
| 3. Показательная | y = a + bx | 
|
| 4. Гипербола | y = a + b 1/x | 
|
| 5. Парабола | y = a + bx + cx2 |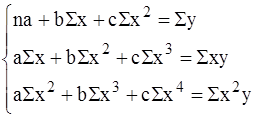 
|
Выбор формы зависимости и определение параметров уравнения регресии (а, b, c) достаточно трудоемкий процесс, поэтому определение регрессионной зависимости желательно выполнять с использованием компьютера.
3.3.6 Дисперсионный анализ
Применяется в тех случаях, когда необходимо ранжировать факторы, формирующие отдельные элементы рынка, по степени их значимости.
Дело в том, что, например, спрос зависит от большого числа факторов – социальных, экономических, демографических, природно-климатических, психологических, эстетических и т.д. Учесть при анализе всю их совокупность, как правило, не представляется возможным. Поэтому в начале выделяют главные, определяющие факторы и проводят их количественный анализ. Влияние остальных, менее значимых факторов, учитывают на качественном уровне.
Ранжирование факторов производится путем расчета коэффициентов детерминации:
,
где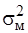 
- межгрупповая дисперсия, вычисленная по данным группировки измеряемого фактора;
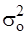- общая дисперсия, характеризующая колебания изучаемого явления.
Чем больше D, тем сильнее фактор влияет на результативный признак.
Пример. Результаты обследования приобретения фермерами сельхозтехники за 5 лет, представлены в следующей таблице.
| Фермеры | Приобретение техники за 5 лет | Доход с 1 га, у.е. | Площадь хозяйства, га |
| 1 | 4 | 750 | 29 |
| 2 | 3,3 | 500 | 35 |
| 3 | 4,2 | 1000 | 39 |
| 4 | 3,1 | 350 | 61 |
| 5 | 4,6 | 1200 | 35 |
| 6 | 3,2 | 400 | 45 |
| 7 | 3,8 | 600 | 70 |
| 8 | 3 | 320 | 65 |
| 9 | 3,9 | 700 | 55 |
| 10 | 4 | 900 | 63 |
| 11 | 3,5 | 450 | 17 |
| 12 | 4,5 | 1100 | 19 |
| 13 | 5 | 2000 | 20 |
| 14 | 4,8 | 1300 | 18 |
| 15 | 4,8 | 1200 | 38 |
Общая дисперсия потребления техники рассчитывается по формуле
,
.
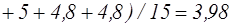Сгруппируем хозяйства по доходам с одного гектара.
| Группы фермерств по доходам с 1га | Среднее потребление техники  по группам
| 
| 
|
| До 500 | 3,22 | -0,76 | 0,5776 |
| 501-1000 | 3,98 | 0 | 0 |
| Свыше 1000 | 4,74 | 0,76 | 0,5776 |
| S | 1,1552 |
.
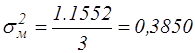Коэффициент детерминации по доходам составляет
.
Теперь сгруппируем по площади в хозяйстве
| Группы фермерств по площади | Среднее потребление техники по группам |
|
|
| До 20 | 4,45 | 0,47 | 0,2209 |
| 21-40 | 4,18 | 0,20 | 0,0400 |
| 41-60 | 3,55 | -0,43 | 0,1849 |
| Свыше 60 | 3,48 | -0,50 | 0,2500 |
| S | 0,6958 |
,
Коэффициент детерминации по площади хозяйств составляет
.
Следовательно, доход с га является в два раза более сильным фактором, влияющим на потребление техники, чем площадь хозяйства.
Поиск по сайту: