Групповые (коллективные) методы выбора решения

К качественным методам в этом плане относятся нижеприве­денные.

Метод голосования (большинством голосов) — применяет ся, если лица, принимающие решения, достаточно компетент­ны в рассматриваемой области. Различается простое (более 1/2 голосов) и квалифицированное (более 2/3 или 3/4) большин­ство. Недостаток метода заключается в том, что не всегда удает­ся обеспечить действительно квалифицированное в рассматри­ваемой области большинство. Так, большинство не склонно принимать инновационные решения.

Метод диктатора — выбирается предпочтение одного ли­ца, например руководителя или наиболее авторитетного специ­алиста. Применяется в чрезвычайных обстоятельствах, когда не удается прийти к согласию при принятии ответственных ре­шений или при недостатке времени для обсуждения проблемы.

Методы согласования мнений экспертов — применяются для получения группового (коллективного) решения. Ранее рассматривался один из методов этой группы — метод Дельфи. Одним из его практических воплощений является деятельность так называемых согласительных комиссий, которые функцио-

нируют, например, в парламентах различных стран, при разра-, белке стандартов в технических комитетах международных ор­ганизаций но стандартизации и др.

Выбор варианта управленческого решения осложняется, ес­ли эксперты (коллеги) образуют коалиции. Коалиции склады­ваются в зависимости от единства интересов людей, их образу­ющих. В коммерческих организациях коалиции образуются чаще всего на основе профессиональных интересов: маркетоло­ги, производственники, конструкторы, технологи, коммерсан­ты и др. В парламентах примерами коалиций могут служить партии и фракции. Коалиция имеет свой статус, который опре­деляется ее авторитетом, властью, полномочиями и ответствен­ностью.

В реальной управленческой практике руководителю часто приходится сталкиваться и работать с коалициями. При приня­тии управленческого решения перед руководителем нередко стоит дилемма: выбрать наиболее эффективный вариант, но из­меняющий статус коалиций, или вариант, учитывающий инте­ресы коалиций. В первом случае велика вероятность нереализа­ции решения, так как коалиции будут саботировать его, во вто­ром — эффект от реализации решения будет незначительным. При принятии решений в условиях коалиций следует руковод­ствоваться нижеприведенными принципами.

Принцип Парето используется тогда, когда эксперты обра­зовали единую коалицию. В качестве решения выбирается ва­риант, который невыгодно менять всем членам группы. Напри­мер, ряд межгосударственных соглашений, установивших пос­левоенные границы в Европе. После Второй мировой войны уже образовалось много новых государств, но все они существуют в установленных послевоенных границах.

Принцип Эджворта применяется тогда, когда эксперты об­разовали несколько коалиций. Здесь выбор варианта решения зависит от характера взаимоотношений с коалициями. При этом рассматривается три ситуации:

1) статус-кво — в качестве решения выбирается вариант, ко­
торый сохраняет статус коалиций;

2) конфронтации — выбирается вариант, который гаранти­
рует выигрыш при наихудших условиях для деятельности и
статуса коалиций;

3) рациональности — выбирается вариант, обеспечивающий
развитие всех коалиций. Каждая коалиция, реализуя управ­
ленческое решение, действует в интересах максимального ре-

зультата для себя, что необязательно наносит ущерб другим ко­алициям.

В ситуации статус-кво руководитель фактически идет на поводу у коалиций. Вероятность реализации такого решения весьма высока, но его эффективность низка. В ситуации кон­фронтации принимается решение вопреки всем или несколь­ким коалициям. В этом случае становится проблематичным воплощение решения в жизнь, а руководитель рискует своим авторитетом (возможно и должностью). Высочайшим искус­ством менеджера является принятие решения, обеспечивающе­го развитие всех коалиций (рациональность). Однако и этот ва­риант не всегда однозначно лучший. Так, неэффективно сохра­нять и пытаться развивать то, что отжило.

Матричные методы выбора оптимального решения^ Один из них — рассмотренный ранее метод минимальной групповой техники. Возможна модификация этого метода, когда пред­ставленные варианты решения проблемы оцениваются особой группой экспертов, при этом их число может не совпадать с чис­лом вариантов.

При многокритериальной задаче вначале производится груп­повая экспертиза вариантов отдельно по каждому критерию, которые затем могут сравниваться по совокупности критериев (например с использованием метода Гилфорта). Более сложный подход предполагает применение специальных математичес­ких моделей обработки результатов экспертизы, учитываю­щих, в частности, степень разброса мнений экспертов (эти мо­дели подробно рассматривются в специальной литературе).

Количественные методы выбора оптимального решения могут использоваться при экспертной количественной оценке решений по одному критерию (эффекта, затрат, времени реали­зации и др.). Пусть, например, два эксперта дали оценку эф­фективности решения следующим образом: оптимистическая -— О, пессимистическая — П. В этом случае при расчете результи­рующей усредненной оценки (Р) пессимистической оценке при­дается больший вес, например, Р = (ЗП + 2О) / 5.

При участии трех экспертов результирующая оценка мо­жет быть рассчитана следующим образом:

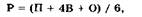
где В — средняя (наиболее вероятная) оценка из трех, данных экспертами, которой придается наибольший вес.

При числе экспертов больше трех может быть использован количественный вариант метода Дельфи. На первом этапе осу­ществляется экспертиза, после чего оценки экспертов (x_i) pac-

полагаются на оси по возрастающей, при этом находятся сред­няя оценка (медиана) и квартили.

На втором этапе экспертам сообщают значения Q1, M и Q₂ и просят пересмотреть оценки, если они выходят за пределы Q1 и Q2- Разброс при этом уменьшается. На третьем этапе экспертам снова сообщают новые Q1, M, q2 и т.д. После того как оценки стабилизируются, значение М принимается в качестве группо­вого решения.

Наукой менеджмента предлагается и ряд других методов выбора оптимального решения. Например, известен метод, ос­нованный на теории ожидаемой стоимости. При этом вариан­ты решений сравниваются по одному критерию, имеющему ко­личественное выражение, но при разных условиях осуществле­ния решений (конъюнктуре рынка, экономическом положении региона и т.д.). Эти условия задаются относительными величи­нами, которые определяют вероятность их реализации. Окон­чательное решение выбирается на основе суммирования про­изведений значений критерия на соответствующие вероятности по каждому из вариантов.

Поиск по сайту: