Свободные электрические колебания

Примером электрической цепи, в которой могут происходить свободные электричес­кие колебания, служит простейший колебательный контур (рис. 1), состоящий из конден­сатора емкостью С и соединенной с ним последовательно катушки индуктивностью L. При замыкании на катушку предварительно заряженного конденсатора в колебательном контуре возникают свободные колебания заряда конденсатора и тока в катушке. Переменное электро­магнитное поле распространяется в пространстве со скоростью, равной скорости света. Поэто­му, если линейные размеры ℓ контура не слишком велики (ℓ << c/ν, где с = 3•108м/с - скорость света в вакууме, ν - частота колебаний в контуре), то можно считать, что в каждый момент времени t сила тока I во всех частях контура одинакова.

Здесь q и φ1–φ2 =- q/C - заряд конденсатора и разность потенциалов его обкладок в произвольный момент времени t; R - электрическое сопротивление колебательного кон­тура, т. е. участка цепи 1- L - 2; ξc= -L(dI/dt)-ЭДС самоиндукции в катушке. Из закона сохранения электрического заряда следует, что сила квазистационарного тока в контуре I=dq/dt. Свободные электрические колебания в колебательном контуре являются гармони­ческими, если его электрическое сопротивление R = 0:

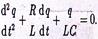(2.1)

Циклическая частота ω и период Т этих колебаний удовлетворяют формуле Томсона:

ω = 1/√LC, (2.2), T=2π√C. (2.3)

Заряд q конденсатора и сила тока I в контуре изменяются по законам: q = q₀sin(ωt + φ₀),

I=I0cos(ωt + φ0) = I0sin(ωt + φ0 + π/2), (2.4)

где q0 - амплитуда заряда конденсатора; I0=ωq0 = q0 /√LC - амплитуда силы тока; φ0 - начальная фаза колебаний заряда конденсатора. Ток в контуре опережает по фазе заряд конденсатора на π/2. Разность потенциалов обкладок конденсатора u = φ2- φ1 также изменяется по гармоническому закону и совпадает по фазе с за­рядом q:

u = U0sin(ωt + φ0),

где U0 = q0/C - амплитуда разности потенциалов. Амплитуда тока

(2.5)

Рис.2.1

При свободных гармонических колебаниях в колебательном контуре происходит периодическое преобразование энергии W_e электрического поля конденсатора в энергию W_m магнитного поля катушки индуктивности и наоборот: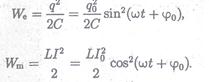

Колебания, происходящие в электрическом колебательном контуре, часто называют электромагнитными колебаниями в контуре. Значения W_e и W_m изменяются при гармонических электромагнитных колебаниях в пре­делах от 0 до максимальных значений, соответственно равных q_o²/(2С) и LI _o²/2, причем, как видно из 27.27), q_o²/(2С)=LI_o²/2. Колебания W_e и W_m сдвинуты по фазе: в те моменты време­ни, когда W_e = 0, W_m = (W_m)_max= LI_o²/2, наоборот, когда W_m= 0,W_е = W_e = (W_е)_max= =q_o²/(2С). Полная энергия электромагнитных колебаний в контуре не изменяется с течением времени:

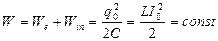
Поиск по сайту: