Стационарное уравнение Шредингера

Для отыскания явного вида волновой функции в квантовой механике необходимо иметь уравнение, подобное уравнению движения Ньютона в классической механике. Такое уравнение было найдено Э. Шредингером в 1926 году. Уравнение Шредингера не выводится, а постулируется на основе известных опытных фактов, и справедливость его доказывается согласием теоретических расчетов и опытных данных. В общем случае уравнение Шредингера имеет вид:

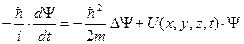, (17.1)

где - масса частицы, Дж×с - постоянная Планка, деленная на , - мнимая единица, - волновая функция, - потенциальная энергия частицы в силовом поле, в котором движется частица, - оператор Лапласа, показывающий, какую операцию нужно провести над волновой функцией . Уравнение (17.1) справедливо для любой частицы, движущейся со скоростью (с - скорость света в вакууме). Уравнение Шредингера накладывает дополнительные условия на волновую функцию :

волновая функция должна быть конечной, непрерывной и однозначной;

волновая функция должна иметь непрерывные частные производные ;

функция должна быть интегрируема, т.е. интеграл должен быть конечным.

Уравнение Шредингера (17.1) не может быть решено в общем случае. Однако, это уравнение можно упростить для тех задач, в которых потенциальная энергия не зависит от времени, т.е. силовое поле, в котором движется частица, стационарное. В этом случае волновую функцию можно представить в виде произведения двух волновых функций: - зависящей только от координат и - зависящей только от времени:

(17.2)

Подставляя (17.2) в уравнение Шредингера (17.1), получим

.

Разделим правую и левую части последнего уравнения на произведение :

. (17.3)

Не трудно заметить, что левая часть уравнения (17.3) зависит только от координат, а правая часть зависит только от времени. Это может удовлетворяться только при единственном условии: если обе части уравнения (17.3) равны постоянной величине Е, которая должна иметь размерность энергии, т.е. являться полной энергией частицы, движущейся в силовом поле и обладающей потенциальной энергией . Получаем два уравнения: первое зависит только от времени

, (17.4)

Второе зависит только от координат (стационарное уравнение Шредингера):

,

которое записывается в следующей форме:

. (17.5)

Стационарное уравнение Шредингера (17.5) в общем случае для произвольной не решается, однако, в некоторых частных случаях можно отыскать решение этого уравнения. Волновые функции, удовлетворяющие уравнению Шредингера при заданном называются собственными функциями, а значения Е, при которых существуют решения уравнения Шредингера называются собственными значениями энергии.

Уравнение (17.4) можно сразу проинтегрировать после разделения переменных:

,

потенцируя последнее выражение, получаем волновую функцию, удовлетворяющую уравнению (17.4):

, (17.6)

где - начальное значение функции .

Поиск по сайту: