Распределение Бозе-Эйнштейна

Рассмотрим систему, состоящую из n невзаимодействующих тождественных фермионов, например, электронов, со спином h/2. Такая система называется идеальным Ферми-газом. В соответствии с принципом Паули в каждой ячейке (в каждом квантовом состоянии) не может быть более двух частиц, причем непременно с антипараллельными спинами. Пусть энергии W_i соответствует g_i ячеек. Для упрощения расчетов можно считать, что в ячейке размером ∆ω/2 может либо находиться одна частица, либо ячейка будет пустой.

Если n_i, число частиц с энергией W_i, получающейся из решения уравнения Шредингера, то энергия системы W и полное число частиц в системе n удовлетворяют условиям:

(20.1)

Найдем число различных способов размещения n_i частиц по g_i ячейкам объемом ∆ω/2. Число различных перестановок всех 0 и 1 будет g_i Число перестановок всех 1 будет n_i!. Число перестановок всех 0 будет (g_i-n_i). Тогда число различных способов указанного размещения:

(20.2)

Общее число различных способов размещения частиц по микросостояниям, соответству­ющее данному макро-состоянию, т.е. термодинамическому состоянию системы, равно про­изведению всех выражений (20.2):

(20.3)

Формула (20.3) определяет термодинамическую вероятность данного макросостояния. Из-за хаотического теплового движения частиц все микро-состояния, соответствую­щие данному макросостоянию, равновероятны, т.е. одинаково часто реализуются в тече­ние достаточно длительного промежутка времени. Поэтому состоянию термодинамического равновесия соответствует максимум Р при выполнении дополнительных условий (20.1). Оказывается, что при достаточно большом числе частиц этот максимум очень острый, т.е. сколько-нибудь значительные отклонения системы от этого равновесного состо­яния весьма маловероятны - возможны лишь малые колебания (флуктуации) около равновесного состояния. Для отыскания условного максимума функции Р удобнее взять функцию In Р и воспользоваться методом неопределенных множителей Лагранжа. Вспомогательная функция имеет вид:

(20.4)

где α и β - постоянные коэффициенты - неопределенные множители Лагранжа. Услов­ный максимум функций ln Р (и Р) соответствует безусловному максимуму функции φ. Из формулы (20.3) следует, что

(20.5)

Воспользуемся приближенной формулой Стирлинга, справедливой при достаточно больших b:

ln b!= b ln b - b (20.6)

Тогда

После простых преобразований выражения ln P функция φ, согласно (20.1) принимает вид:

Дифференцируя эту функцию по n₁ и приравнивая производную нулю, получаем:

Введем обозначение μ = -α/β и перейдем от логарифмов к числам (g_i-n_i)/n_i = e^{β (Wi- μ)}, или окончательно

Формула (20.6) называется распределением Ферми-Дирака. Функция распределения Ферми-Дирака (функция заполнения ячеек), или средняя заселенность фермионами состояний с данной энергией W_i равна:

Аналогичная задача возникает для системы из n невзаимодействующих бозонов с энергией W (идеальный Бозе-газ). Спин бозонов равен нулю или целому числу h, и они не подчиняются принципу Паули. В одной ячейке может находиться произвольное число частиц. Требуется найти число отличных друг от друга размещений частиц по ячейкам μ-пространства, а затем найти наиболее вероятное распределение. Учтем, что энергии W_i соответствуют g_i ячеек и n_i частиц, т.е. (g_i+n_i) элементов. Обозначим ячейки через z₁, z₂, ….., z_gi, а частицы через y₁, y₂, ….., y_gi. Выпишем формально последовательность эле­ментов z и у в произвольном порядке:

z₁, y₁, y₂, z₂, y₃, z₃, y₄, y₅, y₆, z₄, z₅, y₇, …….

Будем считать, что частицы, попавшие между парой элементов z, находятся в той ячей­ке, которая стоит слева от них. В выписанной последовательности частицы y₁ и y₂ нахо­дятся в ячейке z_l, частица у₃ - в ячейке z₂, частицы у₄, у₅ и у₆ - в ячейке z₃, в четвертой ячейке z₄ нет частиц и т.д. Ясно, что первой буквой такого ряда должна быть буква z, а не у. Это можно сделать g_i способами, а оставшиеся (g_i-1+n_i) элементы поcледовательности можно расположить произвольно (g_i+n_l-1)! способами. Полное число различных последовательностей g_i(g_i+n_i-1)!. Однако все последовательности, которые можно получить друг из друга перестанов­кой ячеек или частиц, соответствуют не различным, а одному и тому же состоянию систе­мы. Число таких перестановок g_i n_i. Таким образом, число различных способов размеще­ния n_i частиц по g_i ячейкам в статистике Бозе-Эйнштейна имеет вид

(20.7

Термодинамическая вероятность состояния

(20.8)

Поскольку g_j>> 1, формула (20.8) упрощается:

(20.9^/)

Отыскивать условный максимум будем, как и раньше, для In P:

(20.10)

При получении формулы (20.7) использована формула Стерлинга (20.8). Далее вновь применим метод неопределенных множителей Лагранжа:

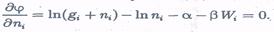
Отсюда

где по-прежнему μ = - α/β.

Следовательно,

(20.11)

Формула (20.11) дает распределение Бозе-Эйнштейна.

Поиск по сайту: