 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Энергия и импульс световых квантов
Электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и химических свойств тела, называется тепловым излучением.
Тепловое излучение тел, находящихся в термодинамическом равновесии, называется равновесным излучением или температурным. В термодинамическом равновесии тепловое излучение, тел компенсируется поглощением такого же количества энергии падающего на него излучения.
Лучеиспускательной способностью Е(v,T) тела называется энергия электромагнитного излучения  изл, испускаемого с единицы площади поверхности тела за единицу времени в интервале частот от
изл, испускаемого с единицы площади поверхности тела за единицу времени в интервале частот от 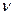 до
до  . Таким образом
. Таким образом
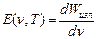 (13.1)
(13.1)
Лучеиспускательная способность в системе СИ выражается в Дж/м2.
Для спектральной характеристики поглощения электромагнитных волн телом вводится понятие поглощательной способности тела  . Поглощательная способность показывает, какая доля энергии
. Поглощательная способность показывает, какая доля энергии  , падающей на единицу площади поверхности тела за единицу времени в интервале частот от
, падающей на единицу площади поверхности тела за единицу времени в интервале частот от 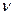 до
до  поглощается телом, т.е.
поглощается телом, т.е.
 (13.2)
(13.2)
Как поглощательная, так и лучеиспускательная способности твердого тела зависят от частоты 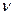 излучаемых или поглощаемых волн, от температуры тела, от его химического состава и состояния поверхности. Если тело полностью поглощает падающую на него энергию электромагнитного излучения при любой температуре и для всех частот, то такое тело называют абсолютно черным. Поглощательная способность абсолютно черного тела по определению равна единице
излучаемых или поглощаемых волн, от температуры тела, от его химического состава и состояния поверхности. Если тело полностью поглощает падающую на него энергию электромагнитного излучения при любой температуре и для всех частот, то такое тело называют абсолютно черным. Поглощательная способность абсолютно черного тела по определению равна единице  .
.
Лучеиспускательная способность абсолютно черного тела  зависит только от частоты
зависит только от частоты 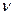 и абсолютной температуры. Реальные тела не являются абсолютно черными. Достаточно хорошим приближением абсолютно черного тела являются сажа, платиновая чернь, черный бархат. Наиболее близкой моде-лью абсолютно черного тела является поверхность малого отверстия в непрозрачной стенке замкнутой полости. При каждом отражении от стенок полости происходит частичное поглощение энергии световой волны и при многократном отражении свет практически не выходит наружу. Запишем связь между электромагнитным излучением
и абсолютной температуры. Реальные тела не являются абсолютно черными. Достаточно хорошим приближением абсолютно черного тела являются сажа, платиновая чернь, черный бархат. Наиболее близкой моде-лью абсолютно черного тела является поверхность малого отверстия в непрозрачной стенке замкнутой полости. При каждом отражении от стенок полости происходит частичное поглощение энергии световой волны и при многократном отражении свет практически не выходит наружу. Запишем связь между электромагнитным излучением  изл, испускаемым с единицы площади поверхности тела за единицу времени в интервале частот от
изл, испускаемым с единицы площади поверхности тела за единицу времени в интервале частот от 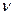 до
до  и спектральной плотностью энергетической светимости
и спектральной плотностью энергетической светимости 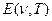 , а также между излучаемой и поглощаемой энергии, исходя из соотношений (13.1) и (13.2):
, а также между излучаемой и поглощаемой энергии, исходя из соотношений (13.1) и (13.2):
 (13.3)
(13.3)
В состоянии термодинамического равновесия  излДля абсолютной черной пластины имеем:
излДля абсолютной черной пластины имеем:
 . (13.4)
. (13.4)
Учитывая, что в состоянии термодинамического равновесия  , окончательно получаем:
, окончательно получаем:
 или
или  (13.5)
(13.5)
Таким образом, отношение лучеиспускательной способности тела к его поглощательной способности не зависит от химического состава тела и равно лучеиспускательной способности абсолютно черного тела и является функцией температуры и частоты  . Этот закон был впервые установлен Кирхгофом и носит его название, а функция
. Этот закон был впервые установлен Кирхгофом и носит его название, а функция  называется функцией Кирхгофа. Из закона Кирхгофа следует, что, если
называется функцией Кирхгофа. Из закона Кирхгофа следует, что, если  , то
, то 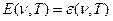 , если
, если  , то
, то  . Следовательно, если тело не поглощает при данной температуре в данном интервале частот, то оно не может и излучать при этой же температуре и этом же интервале частот.
. Следовательно, если тело не поглощает при данной температуре в данном интервале частот, то оно не может и излучать при этой же температуре и этом же интервале частот.
Полная мощность излучения по всему спектру частот от 0 до  называется энергетической светимостью тела или интегральной излучательной способностью, которая обозначается
называется энергетической светимостью тела или интегральной излучательной способностью, которая обозначается  . По определению она равна:
. По определению она равна:

или с учетом закона Кирхгофа
 . (13.6)
. (13.6)
Для абсолютно черного тела  , следовательно:
, следовательно:
 . (13.7)
. (13.7)
В дальнейшем основной задачей теории теплового излучения стало отыскание явного вида функции Кирхгофа. В 1879 году на основе анализа опытных данных Д. Стефан пришел к заключению, что энергетическая светимость любого тела прямо пропорциональна четвертой степени абсолютной температуры. Однако Л. Больцман в 1884 году теоретически методом термодинамики показал, что это утверждение справедливо только абсолютно черных тел. Эта зависимость вошла в историю физики как закон Стефана-Больцмана
 (13.8)
(13.8)
Коэффициент пропорциональности  Вт/м2×К4 носит название постоянной Стефана-Больцмана. Однако они не решили задачу об отыскании явного вида функции Кирхгофа.
Вт/м2×К4 носит название постоянной Стефана-Больцмана. Однако они не решили задачу об отыскании явного вида функции Кирхгофа.
Следующий шаг в нахождении явного вида функции Кирхгофа был предпринят В. Вином в 1893 году, который рассмотрел задачу об адиабатическом сжатии излучения абсолютно черного тела в цилиндрическом сосуде с подвижным зеркальным поршнем и зеркальными стенками. В результате он получил следущее выражение для функции Кирхгофа:
 (13.9)
(13.9)
где  - некоторая неизвестная в явном виде функция.
- некоторая неизвестная в явном виде функция.
Хотя сам В. Вин не установил явного вида функции,  однако из формулы Вина (13.9) вытекает закон Стефана-Больцмана.
однако из формулы Вина (13.9) вытекает закон Стефана-Больцмана.
 |
Из опытов было известно, что зависимость лучеиспускательной способности абсолютно черного тела от частоты при различных температурах имеет вид, показанный на рисунке 13.
Рис. 13.
 |
1 Рис. 13.2
Из этого рисунка видно, что с ростом температуры увеличивается максимальное значение лучеиспускательной способности абсолютно черного тела. Кроме того, сам максимум лучеиспускательной способности черного тела смещается с ростом температуры в сторону более высоких частот. Формула В.Вина позволила сформулировать эти явления в виде законов Вина. При данной температуре частота излучения  , на которую приходится максимум лучеиспускательной способности абсолютно черного тела легко определяется из условия равенства нулю частной производной от функции Кирхгофа:
, на которую приходится максимум лучеиспускательной способности абсолютно черного тела легко определяется из условия равенства нулю частной производной от функции Кирхгофа:
 . (13.10)
. (13.10)
Из последнего равенства следует:
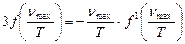
Окончательно получаем закон смещения Вина:
 , (13.11)
, (13.11)
который гласит, что частота, соответствующая максимальному значению лучеиспускательной способности абсолютно черного тела, прямо пропорциональна его абсолютной температуре.  - постоянная величина, зависящая от явного вида функции Вина
- постоянная величина, зависящая от явного вида функции Вина  . Обычно закон смещения Вина записывают через длину волны излучения
. Обычно закон смещения Вина записывают через длину волны излучения
 (13.12)
(13.12)
длина волны, на которую приходиться максимум лучеиспускательной способности абсолютно черного тела с ростом температуры смещается в сторону коротких длин волн. Постоянная 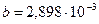 м×К носит название постоянной Вина, определяется опытным путем.
м×К носит название постоянной Вина, определяется опытным путем.
Впервые выражение для функции Кирхгофа было дано в работах Д. Рэлея и Д. Джинса, которые были основаны на представлениях Максвелла и методах статистической физики. Обозначая через  среднее во времени значение энергии осциллятора с собственной частотой при температуре системы Т, можно представить функцию Кирхгофа в виде:
среднее во времени значение энергии осциллятора с собственной частотой при температуре системы Т, можно представить функцию Кирхгофа в виде:
 . (13.14)
. (13.14)
Из, курса классически статистической физики известно, что на одну степень свободы колебательного движения в среднем приходится энергия, равная
 .
.
Подставляя эту энергию в формулу (13.14), окончательно получаем формулу Рэлея и Джинса в вид
 . (14.15)
. (14.15)
Однако формула Рэлея и Джинса достаточно хорошо согласовывалась с опытом только в области низких частот (рис. 13.2).
В области же высоких частот (коротких длин волн) формула Рэлея и Джинса резко расходится с экспериментальными значениями  . Это значительное расхождение теории и опыта при высоких частотах получило название «ультрафиолетовой катастрофы». Кроме того, энергетическая светимость абсолютно черного тела на основе представлений Рэлея и Джинса оказалась равной
. Это значительное расхождение теории и опыта при высоких частотах получило название «ультрафиолетовой катастрофы». Кроме того, энергетическая светимость абсолютно черного тела на основе представлений Рэлея и Джинса оказалась равной
 .
.
Таким образом, формула Рэлея и Джинса находилась в противоречии с законом Стефана-Бoльцмана, согласно которому  . Выход был найден немецким физиком М. Планком в 1990 году. Он не отвергает идеи Рэлея и Джинса об излучении энергии независимыми осцилляторами. Вместе с тем, Планк предположил, что энергия излучения может принимать лишь определенные дискретные значения, равные целому числу элементарных порций энергии - квантов
. Выход был найден немецким физиком М. Планком в 1990 году. Он не отвергает идеи Рэлея и Джинса об излучении энергии независимыми осцилляторами. Вместе с тем, Планк предположил, что энергия излучения может принимать лишь определенные дискретные значения, равные целому числу элементарных порций энергии - квантов  . Следовательно, энергию осциллятора можно представить в виде
. Следовательно, энергию осциллятора можно представить в виде  , где
, где 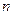 - любое целое положительное число. При этом условии, используя распределение Больцмана, Планку удалось найти среднюю энергию гармонического квантового осциллятора в виде:
- любое целое положительное число. При этом условии, используя распределение Больцмана, Планку удалось найти среднюю энергию гармонического квантового осциллятора в виде:
 . (13.16)
. (13.16)
Подставляя среднее значение энергии гармонического осциллятора в формулу Рэлея и Джинса, получим:
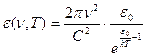 . (13.17)
. (13.17)
Сравнивая эту формулу с формулой Вина (13.9), Планк установил, что энергия кванта должна быть равна  , где
, где  - постоянная Планка.
- постоянная Планка.
 Дж×с
Дж×с
Окончательно Планк получил в явном виде выражение для функции Кирхгофа в виде:
 . (13.18)
. (13.18)
Формула Планка (13.18) для лучеиспускательной способности абсолютно черного тела хорошо согласуется с опытом при самых различных температурах.
Поиск по сайту: