 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифракционная решетка. Принцип Гюйгенса-Френеля
|
Читайте также: |
Принцип Гюйгенса-Френеля. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики.
Дифракцию объясняет принцип Гюйгенса. Именно вторичные волны огибают препятствия на пути распространения первичных волн. Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции (сложения) когерентных вторичных волн, излучаемых вторичными (фиктивными) источниками - бесконечно малыми элементами любой замкнутой поверхности, охватывающей источник S.
 Рассмотрим в произвольной
Рассмотрим в произвольной
Рис.10.1
точке M амплитуду световой волны, распространяющейся в однородной среде из точечного источника S. Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Φ, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Разобьем волновую поверхность Φ на кольцевые зоны такого размера, чтобы расстояния от краев зоны до M отличались на λ/2. Тогда, обозначив амплитуды колебаний от 1-й, 2-й,… m-й зон через A1, A2,… Am (при этом A1>A2>A3> …), получим амплитуду результирующего колебания: А=А1-А2+А3-А4+…
При таком разбиении волновой поверхности на зоны оказывается, что амплитуда колебания Am от некоторой m -й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон  .
.
Тогда результирующая амплитуда в точке M будет:
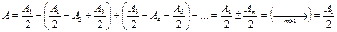 ,
,
 т.к. при m >> 1 A1 >>Am. Площади всех зон Френеля равны
т.к. при m >> 1 A1 >>Am. Площади всех зон Френеля равны  , где
, где  - длина отрезка, SP0 - радиус сферы Φ, b - длина отрезка P0M. Радиус внешней границы m -й зоны Френеля
- длина отрезка, SP0 - радиус сферы Φ, b - длина отрезка P0M. Радиус внешней границы m -й зоны Френеля 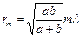 . При
. При  = b =10 см и λ =500 нм радиус первой зоны r=0.158 мм. Следова- тельно, распространение света от S к M
= b =10 см и λ =500 нм радиус первой зоны r=0.158 мм. Следова- тельно, распространение света от S к M
Рис.10.2 происходит так, будто световой поток
распространяется внутри очень узкого канала вдоль SM, т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
Дифракция в сходящихся лучах (дифракция Френеля) - это дифракция сферических волн, осуществляемая в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.
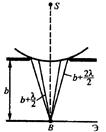
Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Амплитуда света в точке B экрана Э будет A=A1/2±Am/2, где знак " плюс " для случая, когда отверстие открывает нечетное число m зон Френеля, а знак " минус " - для четного m. Дифракционная картина будет иметь вид чередующихся темных и светлых колец с центром в точке B (если m - четное, то центральное кольцо будет темным, если m нечетное, то - светлым).
Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Если диск закрывает первые m зон Френеля, то амплитуда колебания в точке B экрана Э:
 .
.
 Таким образом, в точке B всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами.
Таким образом, в точке B всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами.
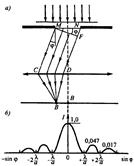
Дифракция в параллельных лучах (Дифракция Фраунгофера). Дифракция Фраунгофера наблюдается в том случае,когда источник света и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию. Параллельный пучок лучей обычно соз
Рис. 10.3 дают, помещая точечный источник света в фокусе собирающей линзы. Дифракционную картину с помощью второй собирающей линзы, установленной за препятствием, фокусируют на экран. Рассмотрим дифракцию Фраунгофера плоской монохроматической волны на одной бесконечно длинной щели шириной a=MN. Оптическая разность хода между крайними лучами MC и ND (см. рисунок): ∆= NF sin aφ. Разобьем открытую часть волновой поверхности MN на зоны Френеля, параллельные ребру M щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, поэтому на ширине щели уместится ∆: λ/2 зон.
 Все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю. Следовательно: 1) если
Все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю. Следовательно: 1) если
Рис.10.4 число зон Френеля четное, то:  ; условие дифракционного минимума; 2) если число зон Френеля нечетное, то
; условие дифракционного минимума; 2) если число зон Френеля нечетное, то  - условие дифракционного максимума, соответствующего действию одной некомпенсированной зоны Френеля. В направлении φ=0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью - центральный дифракционный максимум. Направления, в которых амплитуда максимальна или равна нулю:
- условие дифракционного максимума, соответствующего действию одной некомпенсированной зоны Френеля. В направлении φ=0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью - центральный дифракционный максимум. Направления, в которых амплитуда максимальна или равна нулю:

 .
.
Дифракция Фраунгофера на дифракционной решетке. Одномерная дифракционная решетка - система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.
Распределение интенсивности в дифракционном спектре каждой щели, определяется направлением дифрагированных лучей и дифракционные картины, создаваемые каждой щелью, будут одинаковыми.
 Суммарная дифракционная картина есть результат взаимной интерференции волн, идущих от всех щелей - в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Если Рис. 10.5
Суммарная дифракционная картина есть результат взаимной интерференции волн, идущих от всех щелей - в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Если Рис. 10.5
a - ширина каждой щели b - ширина непрозрачных участков между щелями, то величина d=a+b называется постоянной (периодом) дифракционной решетки.
Разности хода ∆ лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки:
 .
.
Очевидно, что в тех направлениях, в которых ни одно из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях

Кроме того, вследствие взаимной интерференции, в направлениях, определяемых условием

световые лучи, посылаемые двумя соседними щелями, будут гасить друг друга - возникнут дополнительные минимумы. Наоборот, действие одной щели будет усиливать действие другой, если 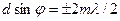 (m=1,2,3,…) - условие главных максимумов.
(m=1,2,3,…) - условие главных максимумов.
Поиск по сайту: