 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Порядок заполнения электронных состоянии
Рассмотрим систему, состоящую из неподвижного ядра с зарядом Zе, и движущегося вокруг него электрона. Если Z = 1, то это атом водорода, при Z>1 система является водородоподобным ионом. В этом случае потенциальная энергия двух взаимодействующих точечных зарядов электрона (е) и ядра (Ze), находящихся на расстоянии r в вакууме, определяется по формуле в вакууме:
 , (19.1)
, (19.1)
е - заряд электрона, ε0 - электрическая постоянная. Графически функция изображена на рис. 19.1. Уравнение Шредингера для этого случая имеет вид:
 (19.2)
(19.2)
Но, учитывая, что поле атома водорода обладает сфе-рической симметрией, уравнение Шредингера целесообразно решать в сферических координатах (r, θ, φ) методом разделения переменных. Как доказывается в теории дифференциальных уравнений, уравнение Шредингера имеет конечные, однозначные и непрерывные решения не всегда, а только при определенных значениях входящих в нее параметров. Одним из параметров является Е - полная энергия электрона. Движение электрона, удовлетворяющее уравнению Шредингера и требованию конечности однозначности и непрерывности волновой функции у, может совершаться только с определенной энергией Е:
 (19.3)
(19.3)
[n = 1,2,3,... — главное квантовое число].
Сравнение выражений (19.3) и (19.1) показывает, что значения энергий, полученные в квантовой механике и по теории Бора, полностью совпадают. Итак, уравнение Шредингера без каких-либо дополнительных гипотез приводит нас к выводу о существовании стационарных состояний атомов, характеризуемых определенной энергией Е. В других состояниях атомы находиться не могут, так как для них уравнение Шредингера не имеет решений, удовлетворяющих стандартным условиям. Уровень энергии, соответствующий минимальному значению энергии El(n=1), называют основным, все остальные Еn(n=2, 3,...) - возбужденными. На рис. 19.1 показаны уровни возможных значений полной энергии атома водорода (E1, E2 и т.д.) в виде горизонтальных прямых и график U(r). С возрастанием главного квантового числа n увеличивается расстояние между электроном и ядром; полная, потенциальная и кинетическая энергии электрона стремятся к нулю. При Е < 0 движение электрона является связанным, он находится внутри потенциальной ямы. Заштрихованная область (Е>0) соответствует состоянию свободного электрона. Из уравнения Шредингера следует, что каждое стационарное состояние электрона в атоме определяется тремя квантовыми числами: n - главным,l - орбитальным, m - магнитным. Никаких постулатов для определения этих чисел не требуется. Квантовые числа n, l и m определяются из свойств ψ-функции, а именно из того, что ψ-функция непрерывна, однозначна и конечна во всем объеме.
Орбитальное квантовое число l определяет модуль орбитального момента импульса электрона, который может иметь лишь дискретные значения, определяемые формулой
 (19.4)
(19.4)
При данном значении n орбитальное квантовое число l может принимать значения 0,1,2,..., n-1. Магнитное квантовое число m определяет проекцию орбитального момента импульса электрона на некоторое произвольно выбранное направление z внешнего магнитного поля:
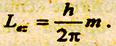 (19.5)
(19.5)
При данном значении l магнитное квантовое число m принимает значения 0, ±1, ±2,..., ±l, т.е. всего (21+1) значени. Величина магнитного момента у атомов и ориентация этого момента в пространстве по отношению к индукции внешнего магнитного поля экспериментально определены впервые в опытах Штерна и Герлаха.

Рис.19.1
На рис. 19.1 изображена схема опытов. Устройство А служило источником атомов. С помощью системы щелей ВВ вырезался узкий пучок атомов, который падал на регистрирующую пластинку CD. На пути пучка создавалось неоднородное магнитное поле SN. Пластинка CD регистрировала расщепление этого пучка на несколько частей. Расщепление пучка в неоднородном магнитом поле - это следствие того, что каждый атом обладает магнитным моментом, поэтому на него со стороны неоднородного магнитного поля действует сила.
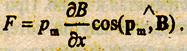
В результате опыта было установлено, что пучок атомов расщепляется на несколько, т.е. cos(pm,B) принимает только определенные дискретные значения, а не любые в пределах от -1 до +1; следовательно, имеет место пространственное квантование. Таким образом, опыты Штерна и Герлаха позволили измерить магнитный момент атома. Однако наблюдались случаи, при которых пучок атомов, проходя неоднородное магнитное поле, расщеплялся на два. Это явление не нашло объяснения ни с точки зрения планетарной модели, ни с квантовой точки зрения.
Голландские физики Уленбек и Гоудсмит в 1925 г. выдвинули гипотезу, согласно которой электрон обладает не только электрическим зарядом, но также магнитным и механическим моментами.
Для описания собственного вращения электрона и соответствующего момента импульса они ввели понятие «спин» (от англ. Spin-вращать). Спином электрона или другой элементарной частицы называют собственный момент импульса.
Этот момент может иметь только две ориентации относительно индукции внешнего магнитного поля. Проекция спина на направление индукции внешнего магнитного поля принимает только два значения:
 (19.6)
(19.6)
ћ= h/(2π); s =±1/2; - спиновое квантовое число. Собственный момент импульса электрона определяется через спиновое квантовое число s по формуле:
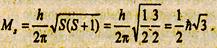 (19.7)
(19.7)
Опытным путем было установлено, что отношение собственного магнитного и механического моментов электрона равно:
 (19.8)
(19.8)
µs, - собственный магнитный момент электрона; m - масса электрона; е - заряд электрона; с - скорость света в вакууме. Подставляя (19.7) в (19.8), определяем собственный магнитный момент:
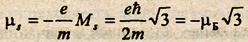 (19.9)
(19.9)
µБ = ећ/2m - магнетон Бора. Физический смысл знака минус в формуле означает, Что механический и магнитный моменты электрона имеют противоположные направления. Проекция собственного магнитного момен-та на направление индукции магнитного поля равна магнетону Бора:
µsz = ±µБ. (19.10
Магнитный и механический моменты электрона проявляются не только в магнитных свойствах вещества, но и в других явлениях, например, наличием спина у электрона объясняются особенности оптических спектров
На основании принципа неразличимости тождественных частиц частицы в квантовой механике делят на два класса состояний, зависящих от природы частиц. В природе существуют частицы, например фотоны и некоторые ядра, обладающие спином, равным h/2π = h. Эти частицы называют бозонами. Частицы, имеющие спин, равный h/4π = ћ/2 называют фермионами. К фермионам относятся электроны, протоны, нейтроны и т. д. Для всех фермионов справедливо утверждение: в системе в одном и том же квантовом состоянии не может находиться более одного фермиона (принцип запрета Паули).
Стационарное квантовое состояние электрона в атоме характеризуется четырьмя квантовыми числами: главным n(n=1,2,3,4), орбитальным l(l= 0,1,2,..., n-1), магнитным m(-l,..., -1,0,1,...,+l), спиновым s(s=±1/2). Принцип Паули: в атоме каждый электрон обладает своим набором квантовых чисел, отличным от набора этих чисел для любого другого электрона.
Общее число электронных состояний, отличающихся хотя бы одним из квантовых чисел, при данном главном квантовом числе равно:
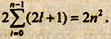 (19.11)
(19.11)
Электроны, занимающие совокупность состояний с одинаковым значением главного квантового числа n, образуют электронную оболочку. Энергия, соответствующая этому квантовому числу, образует уровень энергии. Различают следующие электронные оболочки (или слои):
К-слой при n =1, L-слой при n=2
М-слой при n=3, N-слой при n=4 и т.д.
В каждой квантовой оболочке атома электроны распределяются по подоболочкам, соответствующим определенному значению орбитального квантового числа l; в зависимости от l электрон находится в подгруппе с символами s,p,d,f и т.д. Состояние, характеризуемое n=1, схематически можно изобразить с помощью рис. 19.2.
Как видно из рис. 19.2, в состоянии, определяемом главным квантовым числом n=1, могут находиться лишь два электрона. Электроны, находящиеся в этом состоянии, обладают одинаковой энергией, так как она определяется лишь главным квантовым числом.

Рис.19.2
Таблица 1
| Главное квантовое число | Электронная оболочка | Число электронов в состояниях | Максимальное число электронов | |||
| s (l=0) | p (l=1) | D (l=2) | (l=3) | |||
| K L M N | - | - - | - - - |
Уровень энергии, определяемый главным квантовым числом n =1, называется основным, так как это состояние характеризуется наименьшей энергией и будет реализовываться прежде всего. Если в атоме больше чем два электрона, то другим электронам придется занять энергетический уровень n=2, на котором могут располагаться 2 n2=8 электронов. Если n=2, то схема имеет вид, показанный на рис.19.3. Последовательность заполнения электронных состояний в атомах химических элементов объясняется принципом Паули. Этот принцип дает объяснение периодичности свойств химических элементов в периодической системе, созданной Д.И. Менделеевым в результате изучения физических и химических свойств элементов. Порядок заполнения электронных состояний следующий. Сначала заполняется состояние с наименьшей возможной энергией, затем состояние с более высокой энергией. Для многих атомов это соответствует тому, что сначала заполняется оболочка с меньшим n. В пределах одной оболочки сначала заполняется состояние с l=0, а затем с большим l вплоть до l=n - 1. Для реальных химических элементов справедлив такой порядок заполнения электронных состояний от Z=1 (водород) до Z=18 (аргон) включительно. Нарушение идеального порядка заполнения электронных состояний начинается с Z=19, т.е. калия. Это нарушение связано с взаимодействия между электронами, состояние которых характеризуется главными квантовыми числами n=3, n=4 и т.д. В результате взаимодействия возникает такое положение, что состояние с большим n, но малым l может быть энергетически более выгодным.
Поиск по сайту: