Прохождение частицы сквозь потенциального барьера. (Туннельный эффект)

Рассмотрим задачу об одномерном движении электрона в потенциальной яме. Потенциальной ямой называют зависимость . Реальным примером такого движения является движение коллективизированных электронов в металле, когда вне металла потенциальная энергия электрона равна нулю, а внутри металла она отрицательна и равна численно работе выхода электрона из металла. Вне потенциальной ямы . В потенциальной яме . Ширина потенциальной ямы равна 2 а. Так как движение одномерное вдоль оси ОХ, то волновая функция будет зависеть только от х и учитывая, что , запишем уравнение Шредингера для областей I и III и для областиII:

, (18.1)

. (18.2)

Перепишем уравнение (18.1) в виде:

Обозначим:

(18.3)

Получим уравнение Шредингера для одномерного движения электрона вне потенциальной ямы

. (18.4)

Решением последнего уравнения будет являться волновая функция вида:

(18.5)

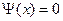Так как волновая функция должна быть конечной для всех , нужно, чтобы А=В=0, т.е. . Смысл полученного решения заключается в том, что вероятность обнаружить электрон равна нулю, т.к. .

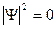Рассмотрим теперь движение электрона внутри потенциальной ямы. Для этого перепишем уравнение (4.2) в виде: , (18.6)

Обозначим:

. (18.7)

Получим уравнение Шредингера для области II, :

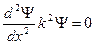. (18.8)

Решением уравнения (18.7) будет являться волновая функция , (18.9)

где и - постоянные коэффициенты, определяемые из граничных условий. Волновая функция должна быть непрерывной, следовательно, на границе областей I и II должно выполняться условие и на границе областей II и III также должно выполняться условие 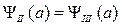. Из условия непрерывности волновой функции на границе потенциальной ямы следует:

. (18.10)

Складывая почленно уравнения (18.10) получим , а это выполняется при 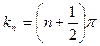, где . Учитывая, что волновое число , после преобразований получаем:

. (18.11)

Последнее означает, что на ширине потенциальной ямы должно укладываться нечетное число полуволн де Бройля. С учетом (18.6) получаем:

. (18.11)

Последнее выражение означает, что электрон в потенциальной яме не может иметь произвольные значения энергии, а будет обладать дискретными значениями энергии, зависящими от целого числа 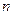. Иначе говоря, электрон в потенциальной яме будет находиться в дискретных энергетических состояниях, в отличие от представлений классической физики.

Вычитая почленно уравнения (18.10), получим . Из последнего выражения следует:

. (18.12)

Из последнего выражения следует, что на ширине потенциальной ямы должно укладываться целое число длин волн де Бройля.

Находим энергию электрона в потенциальной яме с учетом (18.8):

. (18.13)

И в этом случае, так же как и (18.10), энергия принимает дискретные значения. Из полученного решения уравнения Шредингера для электро­на в потенциальной яме можно сделать вывод о том, что энергия элек­трона в потенциальной яме принимает не произвольные значения, а лишь строго дискретные, также как и длины волн де Бройля, электроны.

При рассмотрении данной задачи мы считали, что на границах потенциальной ямы волновая функция становится равной нулю. В дейст­вительности же волны де Бройля электрона на границе потенциальной ямы должны вести себя подобно электромагнитной волне на границе раздела двух сред с различными показателями преломления. Как из­вестно, электромагнитные волны частично отражаются, а частично пре­ломляются, проходя во вторую среду. Подобным образом ведут себя и волны де Бройля на границе потенциальной ямы, т.е. имеется опреде­ленная вероятность обнаружить электрон за пределами потенциальной ямы. Квантовая механика приводит к принципиально новым выводам о движении частиц через потенциальный барьер. Потенциальным барье­ром называется зависимость потенциальной энергии электрона, пока­занная на рисунках (18.2) и (18.3). Для описания движения электрона в таком потенциальном поле вводится понятие прозрачности потенциального барьера, так как возможно просачивание некоторой части электронов с энергией меньшей высоты потенциального барьера сквозь барьер.

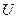
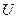
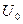
Рис.18.2 Рис.18.3

Прозрачность потенциального барьера в квантовой механике рассматривается как вероятность прохождения волн де Бройля сквозь потенциальный барьер. Вероятность отражения волн де Бройля от потенциального барьера описывается коэффициентом отражения , который будет равен . Прозрачность потенциального барьера зависит от формы потенциального барьера и от его высоты. Не рассматривая вновь решения уравнения Шредингера для одномерного движения электрона сквозь потенциальный барьер, остановимся на выводах.

В случае прямоугольного потенциального барьера высотой 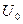и шириной , коэффициент прозрачности вычисляется по формуле:

, (18.14)

где - масса электрона, Е - энергия электрона. Для случая произвольной формы барьера формула коэффициента прозрачности барьера имеет вид:

, (18.15)

где X₁ и Х₂ - координаты начала и конца потенциального барьера, - постоянный коэффициент, близкий к единице. Прохождение частицы, в частности, электрона сквозь потенциальный барьер получило название туннельного эффекта. Туннельный эффект может играть заметную роль в тех случаях, когда прозрачность барьера не слишком мала.

Поиск по сайту: