III. ПЕРВИЧНОЕ ДЕЙСТВИЕ: ДЕЛЕНИЕ ЕДИНИЧНОСТИ

Тот, кто использует геометрические фигуры для описания начала Сотворения, должен попытаться показать, как абсолютная Единичность может стать множественностью и многообразием. Геометрия пытается восстановить упорядоченное движение от бесконечной бесформенности к конечной взаимосвязанной совокупности форм, и при воссоздании этого мистического перехода от Одного к Двум она дает возможность символически увидеть это.

И с метафизической точки зрения, и с точки зрения мира природы будет неправильным утверждать, что для того чтобы прийти к двойке, мы должны взять две единицы и сложить их вместе. Стоит только посмотреть на способ, посредством которого одна живая клетка делится на две. Единица по определению представляет собой единичный элемент, и по причине этого она является Целостностью, а потому включает в себя все. Не может быть двух Единичностей. Единичность, будучи совершенным символом Бога, делит себя внутри себя, создавая таким образом Двойку: «я» и «себя» Бога, так сказать, единичность создателя и созданную множественность.

Созидание, осуществляемое Единичностью, происходит путем деления ее самой, и это может быть отражено геометрически несколькими различными способами в зависимости оттого, каким образом первоначальная Единичность отображается графически. Единичность может соответственно представляться в виде круга, но сама несоизмеримость круга указывает на то, что эта фигура принадлежит к уровню символов, к которому не применимы методы рассуждений и измерений. Единичность можно переопределить как Квадрат, который, обладая совершенной симметрией, также отображает целостность и поддается понятному измерению. В геометрической философии круг является символом непроявленной Единичности, в то время как квадрат отображает Единичность, готовую, так сказать, к воплощению в реальность. Квадрат олицетворяет четыре основных стороны света: север, юг, восток и запад, которые делают пространство понятным, и он образуется двумя парами абсолютно равных, хотя и направленных в разные стороны линейных элементов, таким образом графически описывая вселенскую Природу, которую можно найти в таоизме и других древних философиях.

По определению квадрат образуется четырьмя равными отрезками прямых, соединенных под прямым углом. Но более важным определением является то, что квадратом будет являться результат умножения любого числа на само себя. Операция умножения обозначается крестиком, и этот графический символ сам по себе является точным определением перемножения. Когда мы пересекаем горизонтальную линию вертикальной так, что эти линии имеют одинаковое количество единиц длины, скажем, например, 4, мы видим, что такое пересечение порождает поверхность квадрата: возникает реальная, поддающаяся измерению единица, которая является результатом пересечения. Этот принцип может быть символически распространен на пересечение любых противоположностей, таких как пересечение мужского и женского, что дает рождение отдельному существу, или пересечение основы ткани с уточной нитью, что порождает поверхность холста, или пересечение темноты и света, что дает рождение реальной, видимой форме, или пересечение материи и духа, которое дает рождение самой жизни. Итак, пересечение является принципом действия, который квадрат отображает совершенным образом.

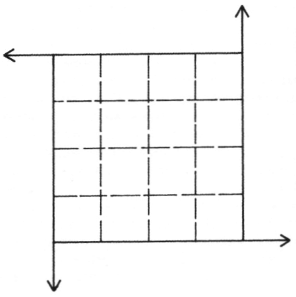	Квадрат есть результат пересечения
Четыре вида ориентации соотносились с четырьмя составляющими Сотворения: землей, воздухом, огнем, водой.

Английское слово Nature (Природа) означает «то, что рождено», и всякое рождение в природе требует такого пересечения противоположностей. Так квадрат стал олицетворением земли, и в качестве такового символизировал сознаваемый опыт конечного существования того, что родилось в Природе. Это приводит нас к вопросу о криволинейности или прямолинейности сторон квадрата: если вся реальность вселенной представляет собой бесконечную кривую, бесконечное движение, то существует все же сознание, которое способно временно приостановить (и концептуально, и чувственно) части вселенского континуума. Это объективное сознание можно рассматривать как приведенную скорость вселенского сознания, средством познания этого объективного сознания является кора головного мозга человека. Индийцы называли такую способность к изолированию и приостановке вечно движущегося вселенского Становления «тапас» («простота»). Греческий философ Гераклит сравнивал ее с параличом видения таким, которое испытывает человек при укусе скорпиона. Он называл объективацию «укусом скорпиона».

Буддистские и индуистские философы были озабочены тем, чтобы такое сегментированное восприятие реальности не завораживало и не поглощало человеческое сознание. Используя известную буддистскую аналогию о времени, которое подобно ожерелью из квадратных бусинок реальных объектов, моментов или событий, можно сказать, что поглощение такой последовательностью ограниченных структур является майей или иллюзией, и только внутренняя нить ожерелья, невообразимый континуум, является реальностью.

Пифагор, тем не менее, учил, что опыт жизни в конечном, ограниченном теле предназначен специально для обнаружения и выявления сверхъестественного существования в пределах конечного. Наша концентрация должна, кроме того, также сосредоточиваться на самом конечном, для того чтобы открыть, как это конечное может, по сути, содержать способность к выражению бесконечного. Это не означает, что концентрация сосредоточивается на конечном, материальном содержании, а на абстрактных принципах, обнаруженных в конечном мире, и на Причинах, которые создают и поддерживают такое овеществление. Поэтому математика Пифагора ограничивалась целыми числами, т.е. поддающимися определению, приостановленными состояниями, и стремилась к универсальным выражениям в рамках измеряемой геометрической структуры квадрата, содержательного символа конечного совершенства.

Приводимая ниже Рабочая книга является первым из девяти подобных разделов, содержащихся в данной книге и предназначенных для того, чтобы читатель шаг за шагом прошел через основные чертежи и концепции Сакральной геометрии. Мы рекомендуем читателю взять циркуль и линейку и самому сделать чертежи каждой фигуры этой Рабочей книги, следуя указаниям, данным рядом с чертежами. Также желательно использовать миллиметровую бумагу для этих чертежей, так чтобы можно было выверить некоторые взаимоотношения простым подсчетом квадратных ячеек на миллиметровке.

Рабочая книга 1
Квадрат, разделенный диагональю √2

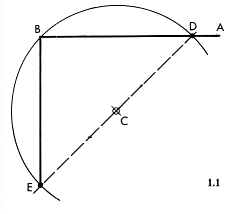
Рисунок 1.1. Начертите любую линию АВ и отметьте какую-либо точку С ниже прямой АВ, где-то ближе к ее середине. Из точки С радиусом СВ начертите дугу, размером по крайней мере с полуокружность, так чтобы прямая АВ пересеклась с этой дугой в точке D. Соедините С и D и продолжите эту линию до тех пор, пока она не пересечет дугу в точке Е. Начертите прямую ЕВ, перпендикулярную к АВ.

Рисунок 1.2. Из центра В радиусом ВА проведите дугу до ее пересечения с BE в точке G. Из центров С и А радиусом АВ начертите две дуги, пересекающиеся в точке F. Начертите квадрат ABGF.

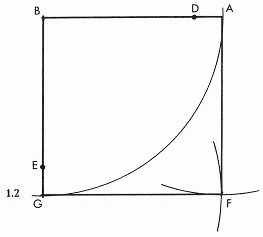
Рисунок 1 .3. В квадрате ABGF начертите диагональ AG. Используя тот же метод, который применялся при построениях на рисунке 1.1, постройте линию из точки G, перпендикулярную к AG. Из центра В радиусом В А проведите дугу, длиной по крайней мере в полуокружность, для получения точек Н и J. Пользуясь тем же методом, который применялся при построениях на рисунке 1.2, завершите квадрат AGHJ.

Сторона квадрата AGHJ (квадрат 2) точно равна диагонали квадрата ABGF (первого квадрата).

Площадь квадрата 2 точно в два раза больше площади первого квадрата. (Это интуитивно очевидно, поскольку больший квадрат содержит четыре одинаковых треугольника, тогда как первый квадрат содержит только два.)

Сторона квадрата называется его основанием или корнем (). Сторона первичного квадрата (квадрат 1) равна 1, а сторона квадрата 2 равна 2.

Диагональ квадрата 2 равна 2, ровно в два раза больше стороны первого квадрата.

Это отношение можно записать следующим образом:

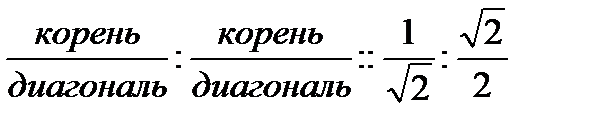
Но это выражение можно записать и так:

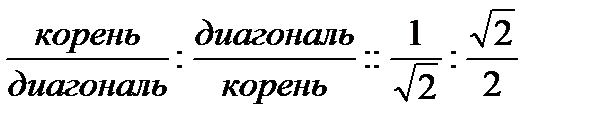
Эти отношения кажутся логическим парадоксом, но если читатель изучит чертеж, он обнаружит, что они геометрически истинны. Даже тогда, когда квадраты увеличиваются в своих размерах, отношения их основания к диагонали остаются пропорциональными.

Рисунок 1.4. Повторите операции, которые были проделаны на Рисунке 1.3. Из центра J начертите дугу, радиус которой равен стороне квадрата 2. Продлите стороны AJ и Ш до тех пор, пока они не пересекут дугу в точках К и М. Начертите квадрат 3, МКНА. Аналогичным образом постройте квадраты 4, 5, и т.д.

Отношение стороны к диагонали каждого квадрата и каждого квадрата к следующему, большему квадрату равно отношению квадрата 1 к квадрату 2. Это отношение можно записать следующим образом:

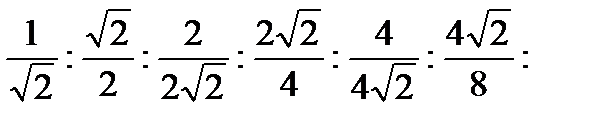и т.д.

или в общем виде:

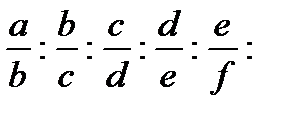и т.д.

Такой тип прогрессии называется геометрической прогрессией, где числитель, будучи умноженным на знаменатель второго отношения, равняется произведению числителя второго отношения на знаменатель первого. Этот закон перекрестного умножения множества числителей и множества знаменателей остается истинным для любых отношений прогрессии, независимо от того, идут они один за другим или нет.

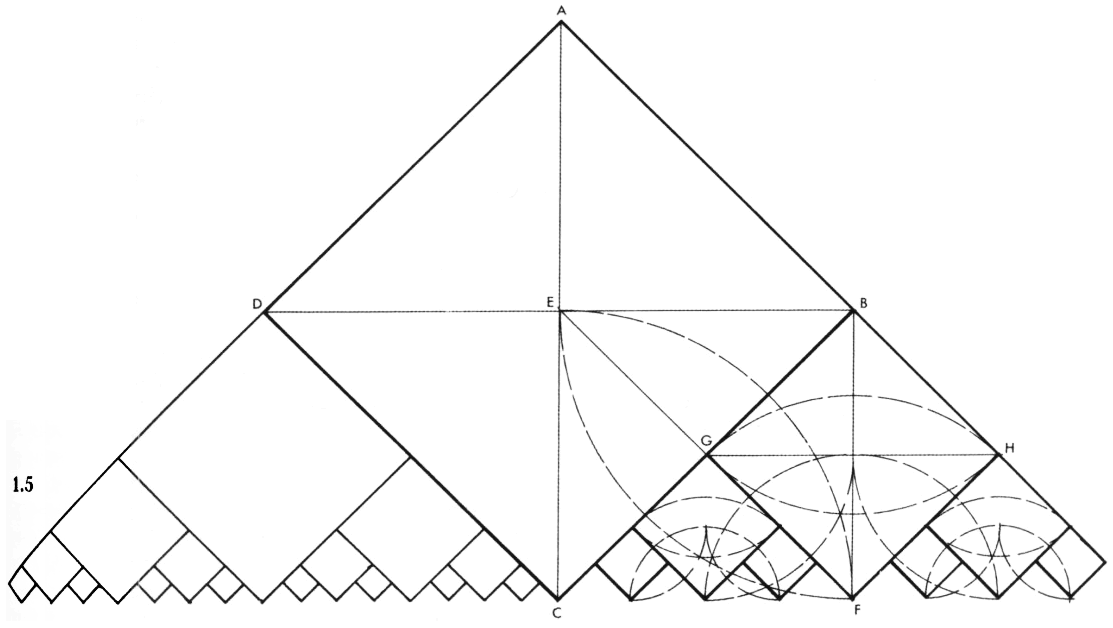
Рисунок 1.5. Здесь представлен вариант предыдущей геометрической прогрессии, но продолженной в сторону убывания. В заданном квадрате ABCD начертите диагонали DB и АС. Из центров в точках В и С радиусом ЕВ, равным половине диагонали, начертите две дуги, пересекающихся в точке F. Начертите прямую EF, пересекающую сторону квадрата 1 в точке G.

Из центров в точках В и F радиусом GF начертите две дуги, пересекающихся в точке Н. Начертите квадрат BHFG (квадрат 2). Повторите этот процесс построения квадратов, которые постепенно уменьшаются в соответствии с геометрической прогрессией: 2, 4, 8, 16, 32 и т.д.

В обоих примерах квадрат и его диагональ отображают создание Двойки из Единичности (первоначальный квадрат) и последующий рост количества в геометрической прогрессии.

Квадрат, разделенный своей диагональю, дает архетипическую модель для геометрических пропорций и прогрессий такого типа: 1: √2:: √2: 2, где каждый член (или отношение) умножается на постоянную величину, для того чтобы получить следующий член прогрессии. Постоянное пропорциональное увеличение или скорость может служить порождающей моделью для других бесконечно расширяющихся геометрических прогрессий, например: 1: √3:: √3: 3 или 1: 3:: 3: 9:: 9:27… и т.д. (смотрите стр. 35). Данная геометрическая иллюстрация отношения между пропорцией и прогрессией вызывает в памяти алхимическую аксиому, говорящую о том, что все создаваемое формируется из неизменного, незыблемого компонента (пропорции), а также из изменяющегося, непостоянного компонента (прогрессии).

Отношение между неизменным и изменяемым (между пропорцией и прогрессией) является ключом к Сакральной геометрии: все, что проявлено, будь это в физическом мире или в мире мысленных образов и концепций, принадлежит к вечно текущим прогрессиям постоянного изменения; и только непроявлен-ный мир Принципов остается неизменным. Наша наука ошибается, пытаясь пристегнуть неизменные, абсолютные законы и определения к изменяющемуся миру явлений. История науки демонстрирует нам постоянный отказ или пересмотр одной модели мира за другой. Из-за вызывающего беспокойство, нестабильного качества научного знания не только наши физики, но также и наши философы, художники и все общество стали релятивистами. Но неизменные порождающие принципы остаются, и наше временное отрицание их имеет место только потому, что мы ищем постоянства в эмпирическом мире вместо его действительного места обитания – метафизического.

Поиск по сайту: