 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Комментарии к Рабочей книге 1
На рисунке 1.3 мы наблюдали деление Единичности, начертив диагональ квадрата. Сторона первоначального квадрата, называемая его «основанием», равна величине в 1 единицу, поскольку она является первой или первичной единицей измерения. Площадь этого квадрата также равна 1, поскольку 1 х 1 = 1. Простое действие проведения диагонали привело нас к 2 не потому, что квадрат стал разделен наполовину, а потому, что имеется в виду квадрат 2, поскольку диагональ квадрата 1 является основанием квадрата 2, и квадрат 2 ровно в два раза больше по площади квадрата 1.
Читатель может резонно задать вопрос: почему, придя к символике квадрата, мы должны затем рассматривать квадрат, построенный на диагонали первого; и если уж на то пошло, зачем рассматривать эту диагональ? Это требуется для того, чтобы мы определили причинно-следственное отношение так, как оно рассматривается в умозрительной геометрии. Как только был нарисован четырехугольник в виде квадрата, в неявном виде мы получили все, что необходимо, для того чтобы начертить линии диагоналей квадрата. Более того, диагональная линия (как и любая прямая линия) является в неявном виде стороной или основанием другого квадрата. Другими словами: мы должны добраться до сути дела или представить в явном виде то, что неявно присутствует в любой геометрической фигуре. Форма представляет собой геометрическую систему, и как любая система – биологическая, химическая или иная – она должна рассматриваться в развертывающемся континууме своих компонентов, в их причинно-следственных взаимоотношениях. Движение от неявного к явному аналогично движению от причины к следствию. И только в условном мире мысли причина может быть отделена от следствия, но в мире природы они неотделимы: причина до тех пор не является причиной, пока у нее нет следствия. Если мы и далее воспользуемся такой логикой, то увидим, что поверхность квадрата также существует только в непрерывном взаимоотношении с объемом куба, в котором она образует одну из шести сторон. В умозрительной геометрии мы всегда пытаемся следовать по всему пути движения от чистой абстракции в виде двумерного мира линии к плоскости по мере того, как она становится проявленной в действительном мире трехмерного объема.
Но вернемся к нашему квадрату: при разделении его диагональю было выявлено два парадокса. Первый заключается в поразительном совпадении двух функций: корня и диагонали, когда мы геометрически извлекали квадратный корень из 2. Та же единица для измерения линии используется и для квадрата, и для диагонали – парадокс сходства и различия. Такая синхронность функций дает три, казалось бы, противоречащих друг другу, но геометрически верных взаимоотношения:

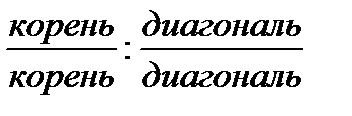

Второй парадокс заключается в том, что половина (квадрат, разделенный пополам своей диагональю) дает удвоение исходного, как при порождении музыкального тона и во время таинства биологического роста при делении клетки.
Квадратный корень из 2 является иррациональной функцией и универсально применимым отношением. Поскольку все в мире природы подвержено изменениям, то этот корень, будучи инвариантным, является по определению сверхъестественным или надрациональным, т.е. он является символом архетип и чес кого мира. Пифагорейцы, как говорят, называли несоизмеримые числа «невыразимыми». Можно с уверенностью говорить о том, что не секретность и не инфантильное благоговение заставило их так называть эти числа. Наоборот, это была глубокая рассудительность интеллекта, осведомленного об отношениях между Числом и космическими реалиями, и умение пользоваться этим.
Рисунок 1.4 показывает, как создание 2 ведет к бесконечному росту посредством геометрической прогрессии а: b :: b: c и т.д. или в числовом виде: 1: 2:: 2: 4:: 4: 8:: 16: 32:: 32: 64 и т.д. Неважно, насколько большими становятся эти числовые взаимоотношения, сама пропорция а: b:: b: с остается неизменной. Эта прогрессия может продолжаться в сторону уменьшения и в сторону увеличения путем деления квадрата пополам с одновременным образованием числового ряда, обусловленного такой способностью диагонали квадрата. Квадратный корень из 2 таким образом олицетворяет способность к множественности, которая может распространяться как в сторону неограниченного увеличения, так и в сторону крайне малых величин. Эта фигура совершенным образом отображает модель роста при клеточном делении в живых организмах. Не только число, но и форма разрастается при разделении Единичности.
Когда мы говорим о квадратных и кубических корнях, мы используем очень древнее обозначение, которое соотносит эту математическую функцию с растительным корнем. Корень растения, как и математический корень, являются причинно-обусловленными понятиями: первый погружен в землю, второй заключен в квадрат. Видимый рост растения, его разрастание с сохранением своей специфики зависит от корня, который обеспечивает стабильность и питание. Способность корня предоставлять растению питание обусловлена тем, что он может разрушать и разделять неподвижные, плотные минеральные элементы почвы с образованием сложных структур, которые растение может преобразовать в свою собственную ткань. С точки зрения жизни геометрический корень является архетипическим выражением ассимилирующей, порождающей, трансформирующей функции, которую и выполняет корень растения. Как и корень растения, корень из 2 наделен природой силой, которая производит разрушение для дальнейшего развития (этому служит первоначальный квадрат), и этот корень также обладает силой, которая мгновенно трансформирует 1 в 2. Рост растения осуществляется прогрессивным образом на основе предыдущего разрушения, но не существует рациональной теории, которая может объяснить, как цветок или кабачок может прорасти из нежного, маленького стебля наподобие скачкообразного роста одного квадрата из другого.
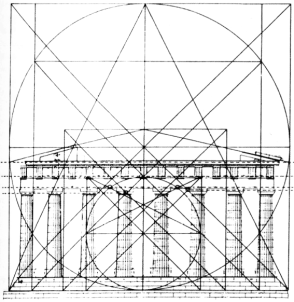
| В этом геометрическом анализе Парфенона, сделанном Тонсом Брюне в его книге Секреты древней геометрии, можно видеть, что его архитектура регулируется отношением между стороной и диагональю ряда квадратов. Каждый квадрат находится во взаимоотношении с большим квадратом, охватывающим его в отношении 1 к 1,25; поэтому вся пропорциональная система основывается на функциональном отношении 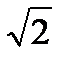 к 1 к 1,25 (или 5/4). к 1 к 1,25 (или 5/4).
|


|
| Указанное выше представляет собой способность к преобразованию, существующую a priori в корне, который и является причиной этого. Принцип корня присутствует в наших телах в виде желудочно-кишечной функции, которая осуществляет трансформацию питательных веществ в энергию. И этот принцип также выражается в виде извилин мозга, который связан с кишечником в том смысле, что он преобразует исходный аморфный мыслительный материал в обоснования и понимание. Фаллическая или воспроизводительная способность в неявном виде присутствует в корне, и сексуальная функция, также как и пищеварительная функция, действует так, чтобы мы укоренились в физическом мире. Мы можем в древней сельскохозяйственной практике сооружения каменных монолитов обнаружить фаллические, ископаемые корни земли, функцию, которая тянет нас назад к плодородному космическому окружению. С другой стороны, молния представляет собой корень неба, трансформирующий углерод и азот в сложные структуры, усвояемые растениями. | 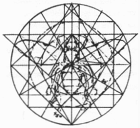 Вездесущее отношение 1:
Вездесущее отношение 1: 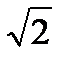 является фундаментальным для дизайна этой исламской напольной мозаики, а также для формы и пропорций медоносной пчелы. является фундаментальным для дизайна этой исламской напольной мозаики, а также для формы и пропорций медоносной пчелы.
|
Если мы разделим всю длину человеческого тела по принципу гармонического деления, соответствующего делению на квадратный корень из 2, приняв всю длину тела за единицу, то обнаружим жизненный центр, соответствующий тому, что японцы называют хара (живот), – трудноуловимый физический центр, расположенный немного ниже пупка. При измерении расстояния от ступней до центра пупка мы получим соотношение 2 – √2, а от центра пупка до макушки головы – соотношение √2 – 1. Этот центр в практике Дзен ассоциируется с медитационной техникой укоренения, включающей активизацию сил физического самоконтроля и самопреобразования. Тантрическое учение в Индии, с другой стороны, стремится к тому, чтобы поднять этого змея или корень таким образом, чтобы он передал свою энергию более высоким, трансформационным гландулярным центрам. Китайская традиция говорит устами Лао-Дзи, который сказал что-то вроде приведенного ниже (мой пересказ):
Не бойся старения тела, поскольку это – путь, посредством которого оно ищет свой корень. Поиск корня – это возвращение к источнику, а возвращение к источнику – это следование за судьбой. Следование за судьбой – благородное дело, а благородство – это мужество, а мужественными являются те, кто стремится к выполнению духовной цели, стоящей за всеми формами. Таким образом, поиск корня – это стремление к этой цели.

| 
| Сходство форм молнии и корня растения является также функционально точным. Наука сегодня строит предположения о том, что в ранние периоды эволюции земли сильные грозы с огромными молниями в атмосфере способствовали образованию обладающего большой энергией ультрафиолетового света, который превращал метановые, водородные, азотные и углеродосодержащие газы в протомолекулы для органических образований сложных структур. Эти молекулы осаждались проливными дождями в первобытные моря, из которых и появилось жизнь. Вновь подчеркнем, что корень функционирует как трансформационный принцип, который поддерживает предрасположенность к росту, которую мы называем жизнью. |
| Корень растет путем постоянного разделения своей квадратной формы. Клетки корня представляют собой сильную метафору к принципу интеграции и трансформации. Геометрическое постижение основывается на идее о том, что естественные формы следует понимать как символы, раскрывающие метафизические архетипические принципы, которые направляют и контролируют эволюцию вселенной. Корень обладает невероятной силой роста, известно, что корни доходят до глубины свыше 100 футов в песках пустыни, чтобы достичь воды. Один куст райграса многолетнего пастбищного может иметь более миллиарда тонких корешков, которые, будучи положены концом к концу, растянутся на 350 миль. Корни агрессивно охотятся и воюют в конкурентной борьбе за воду, воздух и минералы Они должны постоянно выделять кислоты для растворения минералов и обеспечения питательными веществами, а также для защиты растения. Корень служит символом закона самопожертвования в природе, поскольку, подобно матери, его усилия направлены не на достижение собственного благополучия, а на помощь растению в его движении к свету. | Квадратный корень из двух является геометрической функцией, которая олицетворяет вселенскую метафору корня, а сам корень представляет собой принцип трансформации. Этот миг превращения – везде перед нашими глазами: в корнях растений, преобразующих минералы в питательные вещества; в листьях, скалах и камнях, которые под воздействием внешней среды и старения превращаются в молекулярные газы и жидкости, жидкость превращается в газ, газ – в твердое тело, свет – в тепло, тепло – в механическое движение, в прорастание семени. Моллюск преобразует фосфор и натрий в свою кальциевую раковину[*]; усвоение пищи поддерживает образование ментального и духовного опыта. Все находится в состоянии переваривания, усвоения, трансформации. Трансформация осуществляется в каждый проходящий момент, а также в течение длительных эонов эволюционных циклов. Трансформация является повсеместным условием для существующих миров и их эволюции от минерала к растению, а от него – к животному: царство, возникающее из другого царства, объем, формирующий себя из сходящихся векторных удлинений предыдущего объема (см. стр. 72). Везде присутствует периодичность, ритм, колебания, структуры, частота; все можно измерить в единицах пространства и времени. Все это – зарождение последующих явлений, но сам момент трансформации из одного состояния в другое, из одного качества бытия в другое, из одной формы или уровня сознания в другую форму или уровень всегда представляет собой прыжок, скачок, непостижимую скорость, так сказать, за пределами времени, как в случае деления одной клетки на две. Если мы будем рассматривать жизнь или эволюцию только с точки зрения последующего возникновения интеллекта, только с точки зрения рациональной возможности измерения, то реальность зарождения жизни будет всегда ускользать от нас. Этот момент преобразования и есть то, что только и существует; феноменальные миры – это только преходящее отражение. Они представляют собой настоящее и будущее этой одной, всегда существующей вечности, единственной возможной вечности (без продолжительности), которая представляет собой текущий момент. |
Основываясь на наших наблюдениях, полученных из Рабочей книги 1, мы будем рассматривать с философской точки зрения квадрат 1 как олицетворяющий принцип Единичности или то качество абсолютной Единичности, которое отображается в законченности квадрата как единицы, индивидуальности, целостности или системы. Квадрат 2 может аналогичным образом рассматриваться как олицетворяющий Двоичность и способность к росту, т.е. множественность. Когда единица становится двойкой, мы автоматически обладаем потенциалом бесконечной множественности через прогрессию, как мы это и видели. Таким образом, крайняя, очень важная полярность вселенной – Единичность и Множественность – может быть прекрасно представлена и наблюдаема на простом рисунке с изображением квадрата и его диагонали.
| При переходе от одной клетки к двум имеет место цикл изменения, состоящий из восьми фаз на семи интервалах и аналогичный музыкальной октаве или спектру света. Семь является символом таких циклов; в лунном месяце, прекрасном примере последовательных фаз в рамках непрерывного процесса, главную роль играет семерка и ее кратные. Семь в большей степени относится к процессу, чем к форме, поэтому нет простого, естественного способа для изображения семиугольника на окружности. Функциональная модель нервной системы человека также семерична. Начиная с нижней диаграммы: 1 Межсегментарный рефлекс: реакция ограничена возбужденным сегментом. 2 Межсегментарный рефлекс: импульс переносится взаимосвязанными нейронами на соседние сегменты, вызывая скоординированную мышечную реакцию. 3 Уравновешивающий контроль: автоматические реакции выравнивания. 4 Синергетический контроль: автоматический координирующий контроль мышечной деятельности. 5 (a) Слуховые и (b) зрительные рефлексы: автоматические реакции на внезапный шум или вспышки света. 6 Автоматический ассоциированный контроль комплексной мышечной деятельности. 7 Произвольный и тормозящий контроль: выбор реакций с использованием памяти о прошедших опытах. | 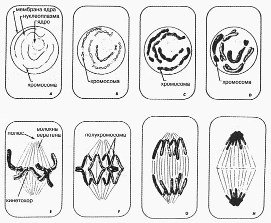
|
 Давайте теперь расширим наше представление о простых, связанных с несоизмеримостью способностях корня как геометрической метафоры к надрациональному моменту трансформации так, чтобы оно включало не только квадратный корень из 2, но и квадратные корни из 3 и 5, как это было сделано во всех известных традициях Сакральной геометрии.
Давайте теперь расширим наше представление о простых, связанных с несоизмеримостью способностях корня как геометрической метафоры к надрациональному моменту трансформации так, чтобы оно включало не только квадратный корень из 2, но и квадратные корни из 3 и 5, как это было сделано во всех известных традициях Сакральной геометрии.
По трем повсеместным процессам можно видеть, как осуществляется такая трансформация: Порождение символизируется квадратным корнем из 2; Развитие символизируется квадратным корнем из 3; и Возрождение символизируется квадратным корнем из 5 и связанной с ним функцией фи (φ). Золотым сечением, которое будет обсуждаться в Главе V.
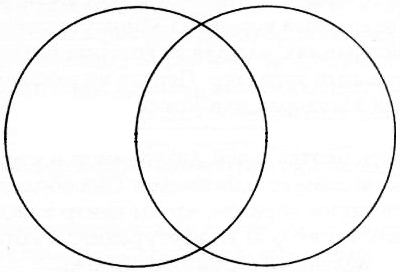
Квадратный корень из 3 присутствует в двух основных геометрических конфигурациях, каждая из которых различным образом проявляет свой созидательный характер. Первая из указанных выше конфигураций, известная как Мандорла или Vesica Piscis (в дословном переводе означает пузырь [vesica], который при наполнении воздухом принимает форму рыбы [piscis]), являлась центральной диаграммой в Сакральной геометрии христианского мистицизма средних веков. Она образуется при начертании двух равных кругов таким образом, чтобы центр каждого из них лежал на окружности другого. Ко второй конфигурации, в которой присутствует √3, относится куб, разделенный своей диагональю.
 Универсальное Равновесное эмпирическое
сознание сознание сознание
СОЛНЕЧНОЕ ЛУННОЕ: отражение
источник: золото серебро
неизменность пропорциональность изменение
сфера архетипов медитация сфера чувств
реальность человеческое соз- действительность
отождествление нание плюрализм
Универсальное Равновесное эмпирическое
сознание сознание сознание
СОЛНЕЧНОЕ ЛУННОЕ: отражение
источник: золото серебро
неизменность пропорциональность изменение
сфера архетипов медитация сфера чувств
реальность человеческое соз- действительность
отождествление нание плюрализм
| 
|
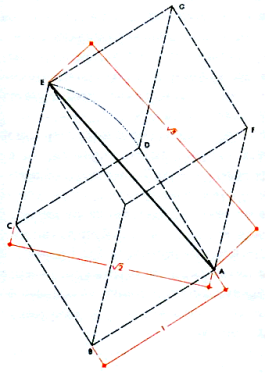
| Один из способов, посредством которого можно увидеть Vesica Piscis, представлен на рисунке в виде промежуточной области, которая включает неизменные и изменяющиеся принципы, вечное и эфемерное. Человеческое сознание, таким образом, действует в качестве посредника, уравновешивающего два дополняющих друг друга полюса сознания. | Куб с гранями, равными 1; треугольная плоскость проходит по диагонали куба. Стороны ED и FB = 1, a EF и DF = 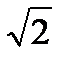 . Поэтому диагональ ЕВ указанной плоскости и куба равна . Поэтому диагональ ЕВ указанной плоскости и куба равна  . .
|
Рабочая книга 2
√3 и мандорла
Рисунок 2.1. Начертите квадрат ABCD (на рисунке он показан повернутым на угол в 30°, так чтобы была видна сравниваемая с ним фигура, расположенная выше). Проведите диагональ СА.
Из точки С начертите линию, перпендикулярную к СА (в отношении используемого метода смотрите Рисунок 1.1). Из центра в точке с радиусом CD, равным 1, проведите дугу до ее пересечения с линией в точке Е. (Обратите внимание на то, что эта операция также показана пунктирной дугой на стороне EGCD куба, показанного вверху.)
Поскольку деление Единичности, символизируемое двумерным квадратом, дает функцию √2, то деление Единичности, символизируемое кубом (который отображает трехмерное пространство) дает функцию √3.
Рисунок 2.2. Построение мандорлы. Начертите круг любого радиуса из любого центра А. Из любой выбранной точки В, расположенной на окружности этого круга, начертите другой круг такого же радиуса.
Поскольку первоначальный круг (Единичность) в точности отображает самого себя вовне в виде второго круга, то между ними образуется общая площадь, определяемая двумя центрами (точками А и В) и пересечением двух окружностей. Эта площадь и форма известны как мандорла или Vesica Piscis.
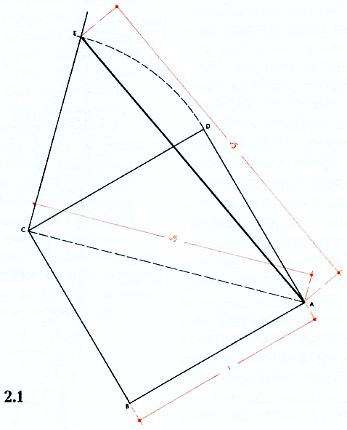

Рисунок 2.3. Геометрическое доказательство наличия пропорции √3 внутри мандорлы. Начертите большую и малую оси CD и АВ. Начертите линии СА, AD, DB и ВС. Начертив дуги выбранного нами ранее радиуса либо из центра А, либо из В, мы пройдем по контуру мандорлы к точкам С и D, убедившись таким образом в том, что линии АВ, ВС, СА, BD и AD равны между собой и равны радиусу, общему для обеих окружностей. Теперь у нас есть два конгруэнтных равносторонних треугольника, образовавшихся в результате наших действий внутри мандорлы. Продлите линии СА и СВ до их пересечения с окружностями А и В в точках G и F. Линии CG и CF являются диаметрами двух кругов и таким образом в два раза больше длины любой из сторон треугольников ABC и ABD. Начертите линию FG, проходящую через точку D.
С использованием такого же метода, что и приведенный выше, мы можем доказать, что FD и GD также равны сторонам треугольников ABC и ABD.
Если АВ = 1, то DG = 1, CG = 2 и по теореме Пифагора 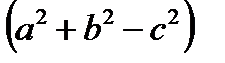 большая ось равна:
большая ось равна: 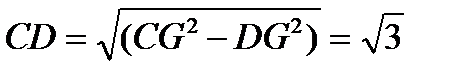 .
.
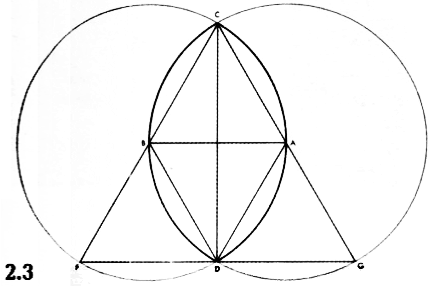
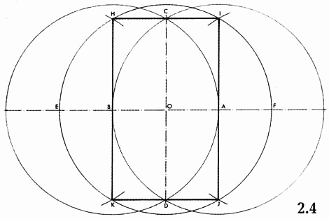
Рисунок 2.4. Геометрическое построение прямоугольника √3. Из точки О, центра мандорлы, начертите третью окружность радиусом 1 и горизонтальную ось, пересекающую все три окружности и пересекающую третью окружность в точках Е и F. Из центров в точках Е и F начертите дуги, не меняя раствор циркуля, так чтобы они пересекали новую окружность в точках Н, I, J и К. Начертите прямоугольник HIJK корня из 3, описывающего мандорлу.
 HI = OI = радиус АВ = 1
HI = OI = радиус АВ = 1
НК = CD = √3
Рисунок 2.5. Построение шестиугольника из мандорлы. Из центра в точке С, полученной при предыдущем построении мандорлы в виде ABCD, проведем дугу изначального радиуса 1 = СВ, так чтобы она пересекла вторую окружность в точке Е. Повторим ту же процедуру из точки D, используя ее в качестве центра, так чтобы дуга пересекла окружность в точке G. Повторим вновь ту же операцию из точки Е или G, так чтобы окружность была пересечена в точке F. Начертим шестиугольник BCEFGD.
Поиск по сайту: