Комментарии к Рабочей книге 4

Если мы начертим диаграмму прогрессии Теона, которая, колеблясь, то сверху, то снизу все ближе подходит к иррациональному центру, то получим общую модель сходящейся волны. Компьютерный анализ показывает, что эти отношения после многих итераций все сильнее приближаются к иррациональному корню, а затем постепенно отходят от этого значения. Мы получаем таким образом общую конфигурацию схождения-расхождения. Можно также нарисовать трехмерную кривую, которая будет выглядеть как спираль, две стороны которой зеркально отображают друг друга, это является таоистским образом отображения движения больших временных циклов.

Рисунок 4.2, основанный на демонстрации Теона, взят из книги Р. А. Шваллера де Любича «Храм человеческий», и он представляет собой модель роста, основанную на корне из 2, которой следуют все процессы в природе. В этой модели обнаруживается точное проявление Принципа Изменения через корень из 2: изменения и в отношении силы – энергетические, причинно обусловленные пульсации надрационального корня, – ив отношении формального колебания квадратов, порожденных этой силой.

Если мы вернемся к нашей таблице отношений корня к стороне: 3 к 2, 7 к 5, 17 к 12, 41 к 29, то увидим, что получаются коэффициенты, которые до пятого или шестого знака дают отношение, равное по точности используемому нами в настоящее время значению корня из 2, мы также увидим, что поступили правильно с функциональной точки зрения, начав эту прогрессию с равных между собой стороны и диагонали. Каждый коэффициент, колеблясь, сначала сверху, затем снизу все сильнее приближается к совершенному иррациональному состоянию. Это является основным элементом того, что мы называем Диофантовой математикой, которая лежит в основании числовых прогрессий, которые можно рассматривать как отображения вибрирующих систем, и в которых вибрирующая струна также движется сверху и снизу абстрактного узла или невидимой неподвижной точки. Мы можем более поэтически представить себе этот процесс как модель пульсации Космической Жизни.

Принцип Изменения служил источником метафизической и физической мудрости во многих великих культурах прошлого. Сегодня мы в наибольшей степени наблюдаем его в таоистской философии, особенно в широко распространенном учении Дзен-буддизма, которое многому обязано этому принципу, а также в принципах Ай Чин.

К иллюстрации Пифагора можно добавить прекрасное понимание сути прироста, данное Р.А. Шваллером де Любичем. Когда корень с его способностью к увеличению, росту и распространению выходит за пределы единичности, он формирует в отношении 1 к 2 остальную свою часть, которая геометрически ведет себя аналогично завязи растения. Я здесь имею в виду принцип корня, обладающего способностью, которую ботаники называют «позитивным геотропизмом», другими словами, способностью к распространению вниз, захвату свободных сфер и трансмутации снизу. Росток, таким образом, наделен способностью к «отрицательному геотропизму» или к тому, что обусловливает рост вверх и в стороны, другими словами, к полному восхождению, кульминацией которого является новое семя. Корень и росток, таким образом, являются полярными противоположностями той же самой способности. Если семя посадить в перевернутом положении, то корень немедленно переориентируется и будет расти вниз, а росток, образующий стебель, перевернется и будет расти вверх. Та-оистский учитель сказал бы в отношении этого, что вся жизнь и вся вселенная развиваются посредством изменений. Истина каждого развития или эволюции состоит в ритмическом изменении и колебании. Все изменяется в сторону своей противоположности. Что касается природного и космического движения, то единственной неотвратимостью является изменение.

Принцип изменения геометрически выражается древним таоистским символом ян и инь. Форма этого символа образуется двумя равными кругами, расположенными внутри большего круга, диаметр каждого малого круга составляет в точности 1/2 большего крута. Отношение диаметра к окружности любого круга равно π C/D = π.

С первого взгляда этот символ предполагает, что деление Единичности (в данном случае она выражается через больший круг, включающий малые) производится на две равные части. Такое деление приводит к статическому равновесию без какой-либо возможности роста. Но именно асимметричное деление, как это было уже проиллюстрировано отношением 1/√2. создает пропорцию, а затем и прогрессию в форме, которую мы называем ростом. Позднее, в главе, посвященной квадратуре круга, мы узнаем об асимметричном принципе, скрывающимся за этим символом. Но важно отметить в данном контексте, что окружность двух внутренних кругов равна окружности большего крута: 2хπD/2 = πD. Эти фигуры демонстрируют продолжение первоначального разделения сначала на 4, а затем и на 8 кругов. Этот процесс деления кругов пополам может осуществляться бесконечным образом, и в любой точке при суммировании окружностей меньших кругов эта сумма будет ровно окружности изначального большого круга. Этот процесс можно довести до такого момента, когда волнистая линия и диаметр станут неотличимыми друг от друга, иллюстрируя таким образом парадокс, заключающийся в равенстве окружности диаметру того же крута. Таким образом, кок и в демонстрации Теона, эта древняя диаграмма показывает, что все развитие в сторону усложнения в своем начале и в своем конце сливается с Единичностью (см. рисунок ниже).

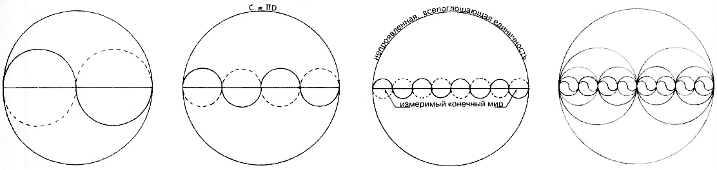
Эта вселенская дихотомия обнаруживается в каждом прорастающем семени. Семя немедленно разделяется на корень и росток. Мы наблюдаем разделение функций: сначала завязь обеспечивает свое собственное питание до тех пор, пока не начнет функционировать корень, затем завязь преобразуется в первые листья, покинувшие оболочку семени, и, наконец, корень принимает на себя функции обеспечения питанием. Эта функция изменения корень/росток геометрически представлена в Рабочей книге 4 (рисунок 4.2), когда корень одного квадрата равен приросту следующего квадрата с повторением аналогичного действия на каждом последующем квадрате. Этот рисунок иллюстрирует сравнение, которое, как и все сравнения в геометрической философии, относится к трехчленному типу пропорции: a: b:: b: с. В этом случае геометрические корень/росток относятся к универсальному принципу корень/росток таким же образом, как этот принцип относится к проявлению отношения корня к завязи в ботанике. С помощью геометрии мы в большей степени исследуем философские принципы, относящиеся к аналогии и пропорциональности, вместо того, чтобы следовать более косной эквациональной логике.

Числа, которые возникают из треугольника Пифагора со сторонами 3, 4, 5, дают прекрасную симметрию для естественных форм. На рисунке показана последовательность, которая начинается с проявления равностороннего треугольника в природе и заканчивается рядом симметричных фигур, вдохновивших мастеров на создание архитектурных шедевров Возрождения, планы первого этажа которых показаны на рисунке.

Поиск по сайту: