X. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ПРОСТРАНСТВ

Восприятие объема дает другую метафору для первоначального и вечно продолжающегося созидающего акта материализации Духа и создания форм. Сам древний миф о сотворении, происходящий из города Гелиополиса, расположенного в Египте, дает пример такого способа воображения. Нун, Космический океан, символизирует чистое, непроявленное дух-пространство без границ и формы. Он предшествует любому распространению, любой конкретности, любому божеству. Он является чистой потенциальностью. Через семя или желание Создателя, который скрыт в этом океане Нун, неразделенное пространство приходит в движение, для того чтобы сжаться и сгуститься с образованием объема. Так Атум, создатель, сначала создает или выделяет себя из неопределенного Нун путем создания объема, для того чтобы начался процесс сотворения.

Какую же форму мог иметь этот первый объем? Какие объемные формы являются наиболее важными? Существует пять объемных форм, которые считаются наиболее важными, поскольку они являются единственными формами, у которых все ребра и все внутренние углы равны между собой. К ним относятся тетраэдр, октаэдр, куб, додекаэдр и икосаэдр, и они являются отображением в объеме соответственно треугольника, квадрата и пятиугольника: 3, 4, 5. Все другие правильные объемные тела получаются путем усечения этих пяти. Эти пять тел называются Платоновыми, потому что предполагается, что Платон уже был знаком с ними, когда писал «Тимея» – диалог, в котором он дает обзор космологии с использованием плоскостной геометрии и геометрии тел. В этом диалоге, который, по сравнению со всеми остальными работами Платона, носит наиболее ярко выраженный пифагорейский характер, он доказывает, что четырьмя базовыми элементами в мире являются земля, воздух, огонь и вода, и что каждый из этих элементов соотносится с одной из пространственных фигур. Традиция связывает куб с землей, тетраэдр с огнем, октаэдр с воздухом и икосаэдр с водой. Платон упоминает «некое пятое построение», использованное создателем при сотворении вселенной. Так додекаэдр стал ассоциироваться с пятым элементом: эфиром (праной). Устроитель вселенной Платона установил порядок из первобытного хаоса этих элементов с помощью основополагающих форм и чисел. Приведение в порядок в соответствии с числом и формой на более высоком уровне привело к предначертанному расположению пяти элементов в физической вселенной. Основополагающие формы и числа затем стали действовать в качестве границы раздела между высшим и низшим мирами. Сами по себе и в силу своей аналогии с другими элементами, они обладали способностью формировать материальный мир.

Как отмечает Гордон Пламмер в своей книге «Математика космического разума», индусская традиция связывает икосаэдр с Пурушей. Пуруша представляет собой семя-образ Брамы, высшего создателя самого себя, и в качестве такового этот образ представляет собой карту или план вселенной. Пуруша является аналогом Космического человека, антропокосмизма западной эзотерической традиции. Икосаэдр представляет собой очевидный выбор для этой первой формы, поскольку все другие тела естественным образом возникают из него.

Пять правильных Платоновых тел.

Тетраэдр	Ребра	Грани	Вершины	Длина
Октаэдр
Куб
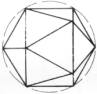
Икосаэдр	Ребра	Грани	Вершины	Длина
Додекаэдр

НА ПРЕДЫДУЩЕЙ СТРАНИЦЕ. Пять правильных многогранников или Платоновых тел использовались, и были известны задолго до времени Платона. Кейт Кричлоу в своей книге «Время остановилось» дает убедительное свидетельство тому, что они были известны людям неолита Британии, по крайней мере, за 1000 лет до Платона. Это заявление основывается на наличии ряда сферических камней, хранящихся в музее Ашмолин в Оксфорде. Эти камни, размеры которых соответствовали тому, что можно уместить в руке, были покрыты геометрически точными сферическими фигурами куба, тетраэдра, октаэдра, икосаэдра и додекаэдра, также как и некоторые дополнительные сложносоставные и псевдоправильные тела, такие как кубо-октаэдр и ико-додекаэдр. Кричлоу говорит: То что у нас ель, представляет собой объекты, несомненно указывающие на степень математических способностей, которые до сих пор отрицались в отношении человека неолита некоторыми археологами или историками математики. Он размышляет о возможной связи этих объектов со строительством больших каменных астрономических колец в Британии, относящихся к той же эпохе:

«Изучение небес связано, кроме всего прочего, с роботами со сферой, которые требуют понимания сферических координат. Если жители неолита Шотландии построили Мейс Хауи до того, кок пирамиды были построены древними египтянами, то почему бы им не изучать законы трехмерных координат? Не является ли то, что Платон, а также Птолемей, Кеплер и Аль-Кинди приписывали космическое значение этим фигурам, не более, чем совпадением?»

Одновременно Люси Пейми в ее ожидаемой книге о египетской системе мер приводит доказательство того, что знанием о данных пяти телах обладали уже в Древнем царстве Египта.

Рабочая книга 9
Платоновы тела

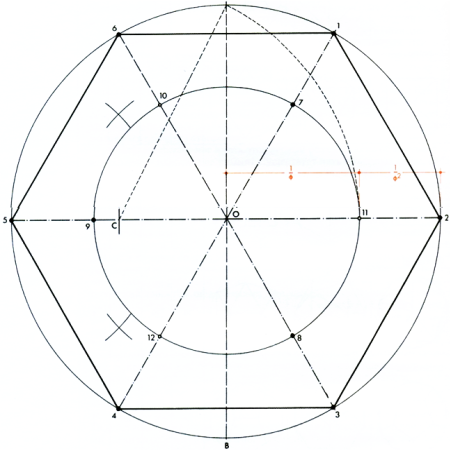
Рисунок 9.1. Одновременное образование Платоновых тел в икосаэдре. Начертите окружность радиусом OA и впишите в нее шестиугольник (2,5) со стороной OA = 1. Проведите вертикальный диаметр АВ. Пометьте каждую вершину шестиугольника цифрами с 1 до 6 и начертите три диагонали 1-4, 2-5, 3-6. Из центра в средней точке С радиусом СА начертите дугу до пересечения с радиусом 0-2 в точке 11. Линия СА = √5/2 разделит радиус 0-2 в соотношении 1/φ и \/φ². Начертите окружность радиусом 0-11 ив местах, где эта окружность пересекает радиусы шестиугольника, сделайте пометки в виде точек и пронумеруйте их с 7 до 12.

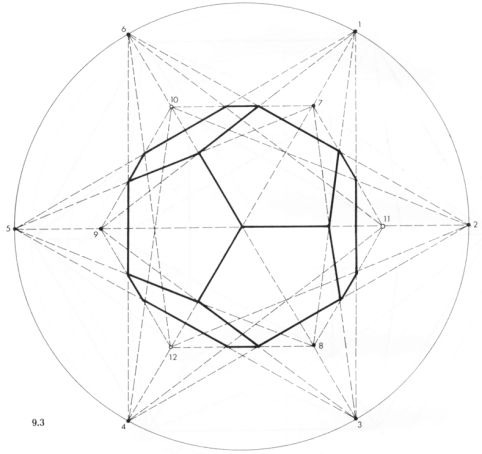
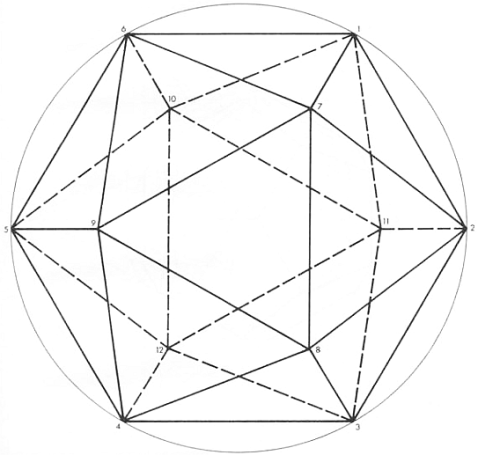Рисунок 9.2. Точки 7, 8 и 9 образуют одну из 20 граней икосаэдра. Эта грань, как и другие 19, представляет собой равносторонний треугольник, показанный здесь в точной пропорции, поскольку он параллелен плоскости рисунка. Грани 7, 8, 2; 8, 9, 4; 9, 7, 6; и 6, 7, 1; 1, 7, 2; 2, 8, 3; 3, 8, 4; 4, 9, 5; и 5, 9, 6 завершают 10 граней, непосредственно видимых нашим глазам. Точки 10, 11, 12 обозначают другую плоскость, видимую в точной пропорции. Она расположена непосредственно напротив плоскости 7, 8, 9, но скрыта от глаз, как и другие 9 плоскостей, отмеченных на рисунке прерывистыми линиями.

Можно видеть, что с помощью φ, «божественного семени», икосаэдр обретает форму.

Рисунок 9.3. Внутри сферы, радиус которой равен радиусу круга из предыдущего рисунка, обозначьте икосаэдр только с помощью его 12 точек. Начертите все связи между 12 вершинами, опустив те из них, которые проходят через центр сферы. Видно, что из каждой точки к противоположной точке можно провести максимум 5 «лучей».

Например, из точки 4 проведите линии 4-10, 4-6, 4-7, 4-2 и 4-11. (В действительности 5 противоположных точек будут задавать правильную пятиугольную плоскость: 10-6-7-2-11, центральная ось которой проходит по диаметру через точку 4.) Повторите то же самое с точками 5,6, 1, 2 и 3, обращайтесь к Рисунку 9.2 как к наглядному примеру. Из точки 8 проведите «лучи» 8-12, 8-5, 8-6, 8-1 и 8-11. Повторите то же самое с точками 9, 7, 11, 12 и 10.

Все множество таких «лучей» будет пересекаться группами по 3 луча в 20 точках пересечения. Эти 20 точек являются вершинами, которые задают додекаэдр, «подвешенный» внутри более крупного икосаэдра. Здесь показаны для ясности шесть видимых граней из 12.

Возникновение додекаэдра происходит спонтанно, как результат естественного пересечения всех внутренних точек-источников икосаэдра. Эти две фигуры являются обратными друг другу: обе состоят из 30 ребер, но, несмотря на это, икосаэдр имеет 20 граней и 12 вершин, а додекаэдр 12 граней и 20 вершин.

Рисунки 9.4, 9.5. Создание додекаэдра автоматически дает нам готовый куб, который определяется 8 вершинами додекаэдра и ребрами, совпадающими с диагональю каждой грани. На рисунке видна верхняя грань 1, 2, 3, 4 и две боковые грани 3, 4, 5, 6 и 1, 4, 5, 7. Диагонали граней этого куба образуют переплетенный или звездообразный тетраэдр. Звездообразный тетраэдр состоит из двух тетраэдров с вершинами, направленными в противоположные стороны; именно эти два тетраэдра и сплетены друг с другом.

Объем, занимаемый этими двумя тетраэдрами, задает октаэдр, что таким образом и завершает эту группу, состоящую из правильных многогранников.

На рисунке куб полностью включает в себя звездообразный тетраэдр. Октаэдр, как и куб, звездообразный тетраэдр и икосаэдр, виден здесь в двумерной перспективе, в плоскости, в виде шестиугольника. Только додекаэдр не входит в наружный контур шестиугольника.

Не только проекции внутренних радиусов икосаэдра образуют ребра додекаэдра, но и аналогично проекция радиуса додекаэдра дает ребро икосаэдра. Такое попеременное получение проекции одной формы из другой здесь обозначено только в виде линий без геометрического доказательства, которое вполне можно провести.

Давайте на словах повторим то, что мы проделали с помощью геометрии. Если мы соединим все внутренние вершины икосаэдра, нарисовав три линии из каждой из них, соединяющих каждую вершину с ей противолежащей, и затем из двух верхних вершин проведем четыре линии к двум противоположным, так чтобы эти линии сошлись в центре, мы, действуя в соответствии со сказанным, естественным образом построим ребра додекаэдра (смотрите Рисунок 9.1 и 9.2). Такое построение происходит автоматически при пересечении внутренних линий икосаэдра. После создания додекаэдра мы можем, просто используя шесть из его вершин и центр, построить куб. Используя диагонали куба, мы можем построить звездообразный или переплетенный тетраэдр. Пересечения звездообразного тетраэдра с кубом дают нам точное местоположение для построения вписанного октаэдра. Затем в самом октаэдре с использованием внутренних линий икосаэдра и вершин октаэдра получается второй икосаэдр. Мы прошли через весь полный цикл, пять этапов от семени к семени. И такие действия представляют собой бесконечную последовательность.

Если размер стороны куба равен 1, то сторона внешнего икосаэдра будет равна 4, а у додекаэдра длина стороны будет равна 1/φ. Длина стороны у переплетенных тетраэдров будет равна √2. Длина стороны октаэдра составит 1/√2, а сторона нового маленького внутреннего икосаэдра будет равна 1/φ²: ошеломляющее созвездие гармоний! Отец (Пуруша) дал рождение самому себе.

Единственным ключом, который необходим, для того чтобы начать такое рисование, является метод, с помощью которого необходимо знать, как находить вершины первого икосаэдра. Он дается нам на радиусе окружности и является результатом деления на φ.

Поиск по сайту: