 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Объяснение демонстрации Теона
Мы начнем данную демонстрацию с теоретического отношения между квадратом и его диагональю: с Единичности (изначальный квадрат, монада), когда и сторона, и диагональ равны 1. Мы продолжим порождение теоретического отношения между стороной и диагональю, следуя модели (данной Теоном), заключающейся в прибавлении стороны к диагонали единичного квадрата, для того, чтобы получить сторону квадрата 2, затем удвоенная сторона первого квадрата прибавляется к диагонали единичного квадрата, для того, чтобы получить диагональ квадрата 2. Первоначальный шаг и сама процедура может на данный момент звучать абсурдно, но примите эту концепцию, и вы увидите, как она работает геометрически.
 КВАДРАТ А-1
КВАДРАТ А-1
диагональ = 1
сторона = 1
Прибавьте величину диагонали квадрата 1 к стороне квадрата 1, для того, чтобы получить сторону квадрата 2: 1 + 1 = 2.
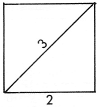 КВАДРАТ А-2
КВАДРАТ А-2
диагональ = 3
сторона = 2
Прибавьте удвоенную сторону квадрата 1 к диагонали, равной 1, для того, чтобы получить диагональ квадрата 2, т.е. 1+2 = 3.

Затем прибавьте величину диагонали квадрата 2 к стороне квадрата 2, для того, чтобы получить сторону квадрата 3: 2 + 3 = 5.
КВАДРАТ А-3
диагональ = 7
сторона = 5
Затем прибавьте удвоенную величину стороны квадрата 2 к диагонали квадрата 2, для того, чтобы получить диагональ квадрата 3:
3 + (2 х 2) = 7.
Отношение стороны к диагонали теоретических квадратов изменится с 1: 1 на 3: 2 и на 7:5. Квадрат 4 будет иметь диагональ равную 7 + (2 х 5) = 17 и сторону 5 + 7 = 12.
Продолжая такое порождение, мы следуем тому же правилу: прибавь величину стороны квадрата к величине диагонали, что дает нам величину стороны следующего большего квадрата, а затем прибавь удвоенное значение стороны к величине диагонали, что даст величину диагонали следующего большего квадрата:
Квадрат 1 2 3 4 5 6
Сторона 1 2 5 12 29 70
диагональ (корень) 1 3 7 17 41 99
Отношение корня к стороне, как это показано ниже: 2:3, 5:7, 12:17, 29:41 и т.д., дает коэффициенты, которые при пятом разложении с высокой точностью до десятых дают нам значение √2 (41/29 = 1,414286…), которое мы используем в настоящее время. Эти коэффициенты, колеблясь, сначала сверху, затем снизу, потом опять сверху всесильнее приближаются к совершенному иррациональному состоянию. Это, в дополнение к ритмическому изменению, ясно выражает концепцию движения в сторону совершенства по мере того, как проявляющиеся аспекты роста все ближе и ближе подходят к обусловившему этот процесс корню. Способность к разделению содержит в себе и способность возвращения к причине, обусловившей это.
| Боковое число | Квадрат | Удвоенный квадрат | Диагональное число | Квадрат на диагональном числе | Разница |
| 2 – 1 | |||||
| 8 + 1 | |||||
| 50 – 1 | |||||
| 288 + 1 | |||||
| 1682 – 1 |
 Эта прогрессия может продолжаться бесконечно, а приведенная выше таблица подтверждает мистическое утверждение Теона о том, что квадрат, построенный на диагонали, всегда будет в два раза больше квадрата, построенного на стороне, но при этом на одну единицу больше или меньше.
Эта прогрессия может продолжаться бесконечно, а приведенная выше таблица подтверждает мистическое утверждение Теона о том, что квадрат, построенный на диагонали, всегда будет в два раза больше квадрата, построенного на стороне, но при этом на одну единицу больше или меньше.
 Рисунки 4. 1 и 4.2. Теоретическая числовая прогрессия отношений стороны к диагонали показана вместе с геометрическим развитием, для того чтобы продемонстрировать графически, насколько быстро последовательность целых чисел приближается к иррациональной функции √2. Из центра в точке А на данном единичном квадрате радиусом АА' проведите дугу, пересекающую ось X в точке В. Из центра в точке Y радиусом YB проведите полуокружность, пересекающую ось Y в точке В'. Из центра в точке В радиусом ВВ' начертите дугу, пересекающую ось X в точке С (5 единиц). Из центра в точке Y радиусом YC начертите полуокружность, пересекающую ось Y в точке C, для того чтобы найти квадрат 3 и его прирост вдоль оси X, повторите те же операции для получения квадратов 4, 5…
Рисунки 4. 1 и 4.2. Теоретическая числовая прогрессия отношений стороны к диагонали показана вместе с геометрическим развитием, для того чтобы продемонстрировать графически, насколько быстро последовательность целых чисел приближается к иррациональной функции √2. Из центра в точке А на данном единичном квадрате радиусом АА' проведите дугу, пересекающую ось X в точке В. Из центра в точке Y радиусом YB проведите полуокружность, пересекающую ось Y в точке В'. Из центра в точке В радиусом ВВ' начертите дугу, пересекающую ось X в точке С (5 единиц). Из центра в точке Y радиусом YC начертите полуокружность, пересекающую ось Y в точке C, для того чтобы найти квадрат 3 и его прирост вдоль оси X, повторите те же операции для получения квадратов 4, 5…
Корень квадрата 1 становится приростом квадрата 2; корень квадрата 2 становится приростом квадрата 5; корень квадрата 5 становится приростом квадрата 12.
Поиск по сайту: