Обчислення

t _А = 2·12·sin30⁰/9,81 = 1,22 с.

t _В = = 2,29 c.

H _max = 12 + (12·sin30⁰)²/(2·9,81) = 13,84 м;

x _max = 12·2,29·cos30⁰ = 23,8 м.

Відповідь: t_А = 1,22 с; t_В = 2,99 с; H _max = 13,84 м; x _max = 23,8 м.

Приклад 3. Тіло обертається навколо нерухомої осі за законом
x = A + Bt + Ct ², де A = 10 рад, B = 20 рад/с, С = –2 рад/с². Знайти повне прискорення точки, що знаходиться на відстані r = 0,1 м від осі обертання, для моменту часу t = 4 с.

Дано: x = A + Bt + Ct ², A = 10 рад, B = 20 рад/с, C = –2 рад/с²; r =
= 0,1 м; t = 4 с.

Знайти: a (t).

Розв’язок. Повне прискорення точки, що рухається по кривій лінії, може бути знайдене як геометрична сума тангенціального прискорення , спрямованого по дотичній до траєкторії, і нормального прискорення , спрямованого до центра кривизни траєкторії (рис. 1.2):

Рис. 1.2.

.

Оскільки вектори і взаємно перпендикулярні, модуль повного прискорення дорівнює

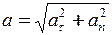. (1)

Модулі тангенціального і нормального прискорень тіла, що обертається, виражаються формулами ; , де – модуль кутової швидкості тіла; – модуль його кутового прискорення.

Підставляючи вираз і у формулу (1), знаходимо

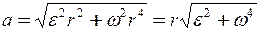. (2)

Кутову швидкість знайдемо, узявши першу похідну кута повороту за часом t: .

Кутове прискорення знайдемо, узявши першу похідну від кутової швидкості за часом: .

У момент часу t = 4 с:

рад/с = 4 рад/с; рад/с².

Поиск по сайту: