 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Обчислення. Приклад 10. У провіднику опором 20 Ом сила струму зростає за лінійним законом від нуля до 6 А за 2 с
|
Читайте также: |
 = 0,58.
= 0,58.
Відповідь: 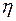 = 58 %.
= 58 %.
Приклад 10. У провіднику опором 20 Ом сила струму зростає за лінійним законом від нуля до 6 А за 2 с. Визначити кількість теплоти, що виділяється в цьому провіднику за першу секунду і за другу секунду. У скільки разів теплота, виділена за другу секунду, більша від теплоти, виділеної за першу секунду?
Дано: R = 20 Ом; t 0 = 0; t k = 2 c; I 0 = 0; I = 6 А;  = 2 c.
= 2 c.
Знайти: Q 1, Q 2, Q 2, Q 1.
Розв’язок. Закон Джоуля-Ленца у виді  справедливий для постійного струму. Якщо сила струму в провіднику змінюється, то цей закон справедливий для нескінченно малого інтервалу часу і записується так
справедливий для постійного струму. Якщо сила струму в провіднику змінюється, то цей закон справедливий для нескінченно малого інтервалу часу і записується так
 . (1)
. (1)
Тут сила струму I є деякою функцією часу  , де k – коефіцієнт пропорційності, що характеризує швидкість зміни сили струму
, де k – коефіцієнт пропорційності, що характеризує швидкість зміни сили струму
 А/с = 3 А/с. (2)
А/с = 3 А/с. (2)
Тоді  .
.
Для визначення теплоти, що виділяється за час Δ t, проінтегруємо цей вираз
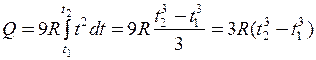 . (3)
. (3)
Тоді
 Дж = 60 Дж;
Дж = 60 Дж;
 Дж = 420 Дж.
Дж = 420 Дж.
Отже, 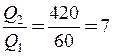 , тобто за другу секунду виділяється теплоти в 7 разів більше, ніж за першу.
, тобто за другу секунду виділяється теплоти в 7 разів більше, ніж за першу.
Відповідь: Q 1 = 60 Дж; Q 2 = 420 Дж; n = 7.
Приклад 11. Визначити силу струму в усіх ділянках кола, вказаного на рис. 3.5, і що включають ЕРС (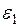 = =  = 3 В, = 3 В,  = 1 В), а також провідники, що мають опори R 1 = 5 Ом, R 2 = 3 Ом, R 3 = 1 Ом. = 1 В), а також провідники, що мають опори R 1 = 5 Ом, R 2 = 3 Ом, R 3 = 1 Ом.
|  Рис. 3.5.
Рис. 3.5.
|
Дано: 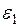 =
=  = 3 В;
= 3 В;  = 1 В; R 1 = 5 Ом; R 2 = 3 Ом; R 3 = 1 Ом.
= 1 В; R 1 = 5 Ом; R 2 = 3 Ом; R 3 = 1 Ом.
Знайти: I 1, I 2, I 3.
Розв’язок. Для розв’язку задачі використовуються закони Кірхгофа. Якщо напрямок струмів вибрати так, як показано на рис. 3.5, то за першим законом Кірхгофа для вузла а одержимо
I 2 – I 1 – I 3 = 0. (1)
За другим законом Кірхгофа для контуру ( ,
,  , R 2 і R 3), лівого на схемі, можна записати рівняння
, R 2 і R 3), лівого на схемі, можна записати рівняння
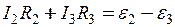 . (2)
. (2)
Для іншого контуру (e 1, R 1 і R 3), правого на схемі, маємо аналогічне рівняння
 . (3)
. (3)
Отримані рівняння являють собою систему трьох рівнянь із трьома невідомими, котру нескладно розв’язати. Зокрема, із другого рівняння можна вивести струм I 2 через струм I 3 і відомі величини, а з третього – струм I 1 через струм I 3 і відомі величини
 ; (4 а)
; (4 а)
 . (4 б)
. (4 б)
Після підстановки цих виразів у перше рівняння легко одержати остаточну формулу для струму I 3
 . (4 в)
. (4 в)
Зробимо обчислення.
 = 0,826 А.
= 0,826 А.
Підставляючи отриманий результат у формули для I 1 і I 2, одержимо
 А;
А;
 А.
А.
Для перевірки отримані результати підставимо у вихідне рівняння, записане за першим законом Кірхгофа
0,391 – (–0,435) – 0,826 = 0.
Таким чином, ми переконалися, що задача розв’язана вірно. Для I 1 отримано негативне значення. Це означає, що в дійсності напрямок даного струму виявився протилежним до того, який було обрано нами довільно (див. рис. 3.5).
Відповідь: I 1 = –0,435 А; I 2 = 0,391 А; I 3 = 0,826 А.
Поиск по сайту: