 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Обчислення. Приклад 6.На плаский повітряний конденсатор подається різниця потенціалів 2 кВ
|
Читайте также: |
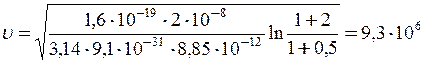м/с.
Відповідь: 
м/с.
Приклад 6. На плаский повітряний конденсатор подається різниця потенціалів 2 кВ. Розміри пластин 40х60 см2, відстань між ними
0,5 см. Після зарядки конденсатор відключають від джерела і потім розсувають пластини так, що відстань між ними збільшується вдвічі. Визначити: роботу з розсування пластин; густину енергії електричного поля до і після розсування обкладок.
Дано: U 1 = 2·103 В; S = 0,24 м2; d 1 = 5·10-3 м; d 2 = 2 d 1; 
= 1.
Знайти: A, w 1, w 2.
Розв’язок. Робота з розсування пластин дорівнює зміні енергії зарядженого конденсатора
A = W 2 – W 1. (1)
Енергія конденсатора визначається формулами
; 
, (2)
де C 1 і C 2 – ємність конденсатора до і після розсування обкладок
; 
. (3)
Вважаючи на те, що конденсатор було відключено від джерела, заряд q на його обкладках не змінився, тобто
q = C 1 U 1 = C 2 U 2. (4)
Підставляючи вираз (3) у (4), легко одержати:
. (5)
Підставивши (2), (3) і (5) у (1), знайдемо:
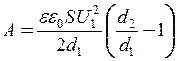. (6)
Об’ємну густину енергії електричного поля в конденсаторі можна знайти, розділивши його енергію на об’єм
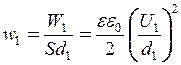; (7 а)
. (7 б)
У даній задачі зв’язок між напругами конденсатора в двох станах виражається формулою (5). Підставляючи її в (7 б) одержимо
. (8)
Поиск по сайту: