Обчислення. Приклад 3. Рентгенівський фотон з довжи

м/с.

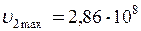Відповідь: м/с; м/с.

Приклад 3. Рентгенівський фотон з довжиною хвилі 0,2·10^{-10 м випробує комптонівське розсіювання на електроні під кутом 900}. Знайти зміну довжини хвилі рентгенівського фотона при розсіюванні, кінетичну енергію електрона віддачі й імпульс електрона віддачі.

Дано: 2·10^{-11 м, 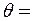900}.

Знайти: , W _к, p _е.

Розв’язок. Зміна довжини хвилі рентгенівських променів при комптонівському розсіюванні визначається формулою

.

Підставивши числові дані, одержимо

м.

Закон збереження енергії , (де – енергія спокою електрона, – повна енергія електрона віддачі), дозволяє знайти кінетичну енергію W _к електрона віддачі як різницю між енергіями первинного фотона і розсіяного фотона

.

Зробимо обчислення.

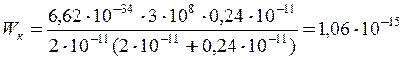Дж.

Імпульс електрона віддачі знайдемо із закону збереження імпульсу. Векторна сума імпульсів розсіяного фотону й електрону віддачі повинна дорівнювати векторові імпульсу первинного фотону (рис. 5.1). З рисунка бачимо, .

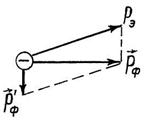Рис. 5.1.

Оскільки і , то вираз для імпульсу електрона віддачі p _е набуває вигляду

.

Зробимо обчислення.

кг·м/с.

Відповідь: = 0,24·10^-11 м; W_к = 1,06·10^-15 Дж; p_е =
= 4,44·10^-23 кг·м/с.

Приклад 4. Паралельний пучок променів з довжиною хвилі
500 нм падає перпендикулярно на зачорнену поверхню, здійснюючи тиск 10^-5 Па. Визначити концентрацію фотонів n ₀ поблизу поверхні і число фотонів n, що падають на одиницю площі за одиницю часу.

Дано: = 5·10^{-7 м; P = 10-5} Па; = 0; S = 1 м²; t = 1 с.

Знайти: n ₀; n.

Розв’язок. 1) Концентрація n ₀ фотонів у світловому потоці може бути знайдена діленням об'ємної густини енергії w на енергію одного фотона , тобто .

З формули для тиску світла випливає, що , а концентрація .

Для зачорненої поверхні коефіцієнт відбиття дорівнює нулю. Підставивши числові дані, одержимо

м^-3.

2) Число фотонів n, що падають на одиницю площі за одиницю часу, чисельно дорівнює відношенню енергетичної освітленості (енергії усіх фотонів, що падають на одиницю площі поверхні в одиницю часу) до енергії одного фотона. Енергетичну освітленість E_e виразимо з формули для тиску світла

,

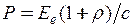звідки 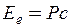(з урахування того, що ). Тоді

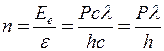
або . Зробимо обчислення.

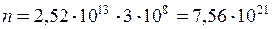м^-2·с^-1.

Відповідь: 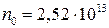м^-3; n = 7,56·10²¹ м^-2·с^-1.

Приклад 5. Електрон в атомі водню перейшов з четвертого енергетичного рівня на другий. Визначити енергію випущеного при цьому фотона.

Дано: n ₁ = 2; n ₂ = 4.

Знайти: .

Розв’язок. Енергія фотона, випущеного при переході електрона з одного енергетичного стану в інший, виражається формулою . Частоту випущеного фотона визначимо за формулою Бальмера

,

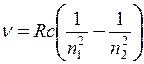де R = 1,097·10⁷ м^-1 – стала Ридберга.

І так,

.

Зробимо обчислення.

Дж.

або 2,54 еВ.

Відповідь: 2,54 еВ.

Приклад 6. Знайти довжину хвилі де Бройля для електрона, що пройшов прискорюючу різницю потенціалів: 1) U ₁ = 51 В; 2) U ₂ =
=510 кВ.

Дано: U ₁ = 51 В; U ₂ = 5,1·10⁵ В.

Знайти: , _.

Розв’язок. Довжина хвилі де Бройля частинки залежить від її імпульсу 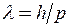. Імпульс частинки можна визначити, якщо відома її кінетична енергія: у нерелятивістському випадку , у релятивістському випадку 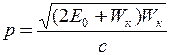, де енергія спокою частинки МеВ. Кінетична енергія електрона, що пройшов прискорюючу різницю потенціалів U ₁: . У першому випадку 51 еВ = 0,51·10^-4 МеВ, тобто W _1к<< E ₀ і значить .

Зробимо обчислення.

м.

В другому випадку кінетична енергія W _2к = 510 кеВ = 0,51 МеВ, тобто дорівнює енергії спокою електрона. Тому необхідно застосувати релятивістську формулу для імпульсу . Оскільки 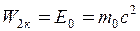, то перепишемо формулу

.

Зробимо розрахунок.

м.

Відповідь: 1,71·10^-10 м; 1,4·10^-12 м.

Приклад 7. Кінетична енергія електрона в атомі водню має величину порядку 10 еВ. Використовуючи співвідношення невизначеностей, оцінити мінімальні лінійні розміри атома.

Дано: W _к = 10 еВ = 1,6·10^-18 Дж.

Знайти: l _min.

Розв’язок. Із співвідношення невизначеностей 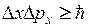випливає, що чим точніше визначається положення частинки в просторі, тим більше невизначеним стає імпульс, а отже, і енергія частинки. Якщо атом має лінійні розміри l, то електрон атома буде знаходитися десь у межах цієї ділянки. При цьому невизначеність координати електрона дорівнює . Співвідношення невизначеностей можна переписати у вигляді 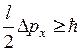, звідки 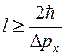. Фізично розумна невизначеність імпульсу Δ p_x не повинна перевищувати значення самого імпульсу p, тобто 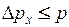. Імпульс пов’язаний з кінетичною енергією: . Тоді .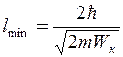

Зробимо обчислення.

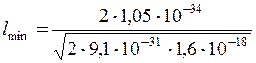= 1,23·10^{-10 м.}

Відповідь: = 1,23·10^{-10 м.}

Приклад 8. Електрон в одномірній прямокутній нескінченно глибокій «потенціальній ямі» шириною l знаходиться в збудженому стані (n = 2). Визначити імовірність виявлення електрона в середній третині «ями».

Дано: ; ; .

Знайти: w.

Розв’язок. Імовірність w виявлення частки в інтервалі визначається формулою

,

де Ψ_т(x) – нормована власна хвильова функція, що відповідає даному стану,

.

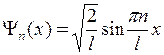Збуджений стан (n = 2) описує функція

.

Тоді імовірність .

Проінтегрувавши цей вираз в межах від до , одержимо .

Відповідь: w = 0,192.

Приклад 9. Маса препарату радіоактивного магнію ₁₂Mg²⁷ дорівнює 0,2 мкг. Визначити початкову активність препарату і його активність через 1 годину. Період піврозпаду радіоактивного ізотопу магнію ₁₂Mg²⁷ дорівнює 10 хв.

Дано: m = 0,2·10^{-9 кг; t = 1 година; T} _1/2 = 10 хв.; t ₀ = 0.

Знайти: A ₀; A (t).

Розв’язок. Активність препарату зменшується згодом по експоненціальному закону , де – початкова активність препарату у момент часу t = 0. Стала радіоактивного розпаду 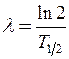. Кількість атомів у препараті у початковий момент часу .

Таким чином, початкова активність . Зробивши підстановку числових даних, одержимо

Бк,

або

Ки.

Тоді активність препарату через t = 1 година = 60 хв. складе

.

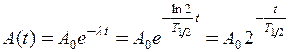Підставивши числові дані, одержимо

Ки.

Відповідь: A ₀ = 139 Ки; A (t) = 2,17 Ки.

Приклад 10. Обчислити дефект маси та енергію зв’язку ядра бора ₅B¹¹.

Дано: m _в = 11,00931 а.о.м.; m_н = 1,00783 а.о.м.; m _n = 1,00867 а.о.м.

Знайти: Δ m; Δ E _зв..

Розв’язок. Дефект маси ядра

.

У зв’язку з тим, що в довідкових таблицях завжди даються маси нейтральних атомів m_а, а не ядра m _я, наведену формулу слід перетворити. Оскільки m _я = m_а – Zm _e, то . Вважаючи, що , де m – маса атома водню, остаточно знаходимо

.

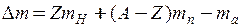Підставивши значення, одержимо

= 0,08186 а.о.м.

Енергія зв’язку ядра знаходимо із закону взаємозв’язку маси й енергії . Якщо обчислювати енергію зв’язку, користуючись позасистемними одиницями, то c ² = 931 МеВ/а.о.м. З обліком цього формула приймає вигляд 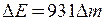(МеВ). Підставивши знайдене значення дефекту маси, одержимо

МеВ.

Відповідь: = 0,08186 а.о.м.; 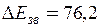МеВ.

Приклад 11. Знайти, яке ядро утвориться у результаті ядерної реакції й обчислити енергію цієї реакції.

Розв’язок. Використовуючи закон збереження маси і заряду, одержуємо

4 + 10 = 1 + A, 2 + 5 = 1 + Z, тобто

і ядерна реакція буде виглядати так

.

Енергетичний ефект ядерної реакції визначається формулою

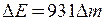(МеВ),

де 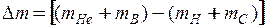– дефект маси ядерної реакції в а.о.м.

Значення мас нейтральних атомів наведені в довідкових таблицях:

а.о.м. а.о.м.

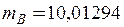а.о.м. 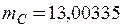а.о.м.

Підставивши числові дані, одержимо

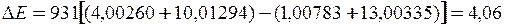МеВ.

Оскільки Δ m >0, реакція є екзотермічною і йде з виділенням енергії.

Відповідь: Δ Е = 4,06 МеВ.

Приклад 12. Визначити теплоту, необхідну для нагрівання кристала NaCl масою 20 г від температури 2 К до температури 4 К. Характеристичну температуру Дебая 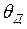для NaCl прийняти рівною 320 К и умову вважати здійсненою.

Дано: m = 2·10^{-2 кг; T} ₁ = 2 К; T ₂ = 4 К; 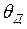= 320 К;
= 58,5·10^-3 кг/моль.

Знайти: Δ Q.

Розв’язок. Теплота Δ Q, що підводиться для нагрівання тіла від температури T ₁ до T ₂, може бути обчислена за формулою

,

де C_T – теплоємність тіла, що пов’язана з молярною теплоємністю співвідношенням . У свою чергу молярна теплоємність при низьких температурах (T << θ _Д) визначається формулою

,

де R = 8,31 Дж/(моль·К) – універсальна газова стала.

Підставляючи теплоємність у формулу для Δ Q, одержимо

.

Перетворимо отриману формулу і зробимо обчислення

;

Дж.

Відповідь: Дж.

Приклад 13. Кремнієвий зразок нагрівають від 0 ⁰С до 10 ⁰С. У скільки разів зростає його питома провідність?

Дано: t ₁ = 0 ⁰С; t ₂ = 10 ⁰С.

Знайти: .

Розв’язок. Питома провідність власних напівпровідниках пов’язана з температурою T співвідношенням

,

де 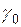– константа; Δ E – ширина забороненої зони; k = 1,38·10^-23 Дж/К – стала Больцмана. Отже,

.

Покладаючи для кремнію Δ E = 1,1 еВ, зробимо обчислення:

.

Відповідь: .

Поиск по сайту: