 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Обчислення. Приклад 2. Два точкові електричні заряди 1 нКл і –2 нКл знаходяться у повітрі на відстані 10 см один від одного
|
Читайте также: |
 = 5,77·10-9 Кл.
= 5,77·10-9 Кл.
Відповідь: q 4 = 5,77·10-9 Кл.
Приклад 2. Два точкові електричні заряди 1 нКл і –2 нКл знаходяться у повітрі на відстані 10 см один від одного. Визначити напруженість і потенціал електричного поля, створюваного цими зарядами, у точці, віддаленій від першого заряду на 9 см і від другого – на 7 см.
Дано: q 1= 10-9 Кл; q 2= –2·10-9 Кл; d = 0,1 м; r 1= 9·10-2 м; r 2= 7·10-2 м.
Знайти: E;  .
.
Розв’язок. Відповідно до принципу суперпозиції, напруженість електричного поля  в пошукуваній точці дорівнює векторній сумі полів
в пошукуваній точці дорівнює векторній сумі полів  і
і 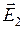 , створених кожним зарядом q 1 і q 2 окремо
, створених кожним зарядом q 1 і q 2 окремо
 , (1)
, (1)
де
 ; (2 а)
; (2 а)
 . (2 б)
. (2 б)
Вектор  (рис. 3.2) спрямований уздовж силової лінії від заряду
(рис. 3.2) спрямований уздовж силової лінії від заряду
q 1, оскільки цей заряд позитивний; вектор 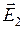 спрямований за силовою лінії до заряду q 2, тому що цей заряд негативний. Модуль результуючого вектора спрямований за силовою лінії до заряду q 2, тому що цей заряд негативний. Модуль результуючого вектора  знайдемо за теоремою косинусів знайдемо за теоремою косинусів
 . (3) . (3)
|  Рис. 3.2.
Рис. 3.2.
|
Тут  – кут між векторами
– кут між векторами  і
і 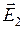 , що може бути також визначений за теоремою косинусів із трикутника, утвореного сторонами d, r 1 і r 2
, що може бути також визначений за теоремою косинусів із трикутника, утвореного сторонами d, r 1 і r 2
 . (4)
. (4)
Підставляючи в (3) вираз (2) і (4), одержимо
 . (5)
. (5)
Потенціал результуючого поля, відповідно до принципу суперпозиції, дорівнює алгебраїчній сумі потенціалів
 . (6)
. (6)
Тут 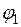 і
і  – потенціали полів точкових зарядів q 1 і q 2 у пошукуваній точці
– потенціали полів точкових зарядів q 1 і q 2 у пошукуваній точці
 ; (7 а)
; (7 а)
 . (7 б)
. (7 б)
Таким чином, з (6) і (7) одержимо
 , (8)
, (8)
де варто враховувати знаки зарядів q 1 і q 2.
При обчисленнях візьмемо до уваги, що в одиницях СІ загальний множник виразів (5) і (8) дорівнює
 = 9·109 м/Ф.
= 9·109 м/Ф.
Обчислення.
 = 3,58·103 В/м;
= 3,58·103 В/м;
 В.
В.
Відповідь: E = 3,58·103 В/м;  В.
В.
Приклад 3. Уздовж тонкого кільця рівномірно розподілений заряд у 40 нКл з лінійною густиною 50 нКл/м. Визначити напруженість електричного поля, створеного цим зарядом у точці, що лежить на осі кільця і віддалена від його центра на відстань, що дорівнює половині радіуса.
Дано: q = 4·10-8 Кл; 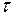 = 5·10-8 Кл/м; h = R /2.
= 5·10-8 Кл/м; h = R /2.
Знайти: E.
Розв’язок. Виділимо на кільці малу ділянку довжиною dl (рис. 3.3). Оскільки заряд dq 1 = 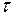 dl, який знаходиться на цій ділянці, вважається точковим, то напруженість електричного поля dl, який знаходиться на цій ділянці, вважається точковим, то напруженість електричного поля  , що створено цим зарядом, можна записати у вид , що створено цим зарядом, можна записати у вид
 . (1) . (1)
|  Рис. 3.3.
Рис. 3.3.
|
Розкладемо вектор  на дві складові:
на дві складові:  , перпендикулярну площини кільця, і
, перпендикулярну площини кільця, і  , паралельну до площини кільця, тобто
, паралельну до площини кільця, тобто
 . (2)
. (2)
Напруженість E електричного поля в пошукуваній точці знайдемо інтегруванням
 ,
,
де інтегрування ведеться по всіх елементах зарядженого кільця. З рисунка бачимо, що для кожної пари зарядів dq і dq ′, розташованих симетрично щодо центра кільця, складові  і
і  однакові за модулем і протилежні за напрямком:
однакові за модулем і протилежні за напрямком:  . Тому векторна сума
. Тому векторна сума  . Складові
. Складові  для всіх елементів кільця напрямлені уздовж осі кільця, тому
для всіх елементів кільця напрямлені уздовж осі кільця, тому
 , (3)
, (3)
де 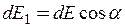 , або з урахуванням (1)
, або з урахуванням (1)  ,
, 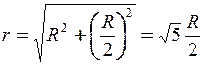 ,
,  .
.
З урахуванням цього
 . (4)
. (4)
Із співвідношення  визначимо радіус кільця
визначимо радіус кільця  . Тоді
. Тоді
 . (5)
. (5)
Зробимо обчислення.
 = 7,92·103 В/м.
= 7,92·103 В/м.
Відповідь: E = 7,92·103 В/м.
Приклад 4. Нескінченна площина, розташована вертикально, заряджена рівномірно з поверхневою густиною заряду 40 мкКл/м2. На шовковій нитці, один з кінців якої закріплений у точці на цій площині, підвішена кулька масою 1 г, що несе заряд 1 нКл. Який кут із площиною утворить нитка, на якій висить кулька?
Дано: 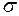 = 4·10-5 Кл/м2; q = 10-9 Кл; m = 10-3 кг.
= 4·10-5 Кл/м2; q = 10-9 Кл; m = 10-3 кг.
Знайти:  .
.
Розв’язок. У стані рівноваги результуюча усіх сил, що діють на кульку (рис. 3.4), дорівнює нулю
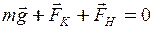 . (1)
. (1)
Тут  , ,  і і  – відповідно сила ваги, сила кулонівського відштовхування і сила натягу нитки.
Векторна сума взаємно перпендикулярних сил – відповідно сила ваги, сила кулонівського відштовхування і сила натягу нитки.
Векторна сума взаємно перпендикулярних сил  і і  (на рис. 3.4 – сила (на рис. 3.4 – сила  ) спрямована уздовж нитки і в стані рівноваги урівноважується силою ) спрямована уздовж нитки і в стані рівноваги урівноважується силою  . З цього випливає, що пошукуваний кут дорівнює кутові між векторами . З цього випливає, що пошукуваний кут дорівнює кутові між векторами  і і  , тому , тому
|
 Рис. 3.4.
Рис. 3.4.
|
 . (2)
. (2)
Кулонівська сила, що діє на заряджену кульку в однорідному електричному полі площини, дорівнює
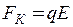 . (3)
. (3)
Тут E – напруженість електричного поля, створювана рівномірно зарядженою площиною
 . (4)
. (4)
Таким чином, з (2)–(4) можна одержати остаточний вираз для пошукуваного кута
 . (5)
. (5)
Поиск по сайту: