АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Приклади розв’язку задач

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Решение логических задач средствами алгебры логики
  3. I. Розв’язати задачі
  4. I. Ситуационные задачи и тестовые задания.
  5. II. Основные задачи и функции
  6. II. Решение логических задач табличным способом
  7. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  8. II. Цель и задачи государственной политики в области развития инновационной системы
  9. III. Решение логических задач с помощью рассуждений
  10. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  11. IV. Определите, какую задачу взаимодействия с практическим психологом поставил перед собой клиент.
  12. IV. Розв’язати задачі

 

Приклад 1. Рівняння руху матеріальної точки уздовж осі має вид , де A = 2 м, B = –2 м/с, C = 0,5 м/с3. Знайти координату, швидкість і прискорення точки в момент часу t = 3 с. Знайти середні значення швидкості і прискорення у проміжок часу від 1 с до 3 с.

Дано: ; A = 2 м, B = –2 м/с, C = 0,5 м/с3; t = 3 с,
t 1 = 1c, t 2 = 3 c.

Знайти: , , , , .

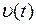Розв’язок. Координату х знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В, С і часу t.

Миттєва швидкість щодо осі х – це перша похідна від координати за часом:

. (1)

Миттєве прискорення точки знайдемо, узявши першу похідну від швидкості за часом:

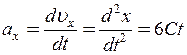. (2)

Обчислення.

Для моменту часу t = 2 с одержимо

x = (2 – 2ּ3 + 0,5·33) (м) = 9,5 м;

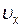= (–2 + 3·0,5·32) м/с= 11,5 м/с;

a 1 = (6·0,5·3)м/с2 = 9 м/с2.

Середня швидкість визначається відношенням

,

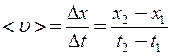де х 1 = 2 – 2 t 1 + 0,5 t 13 = 0,5 м; х 2 = 2 – 2 t 2 + 0,5 t 23 = 9,5 м/с.

Тоді

м/с.

Середнє прискорення визначається за формулою 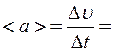, згідно (1)

–2 + 3·0,5 = –0,5 м/с, –2 +3·0,5 = 11,5 м/с.

Тоді

м/с2.

Відповідь: x = 9,5 м; 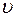= 4,5 м/с; a = 6 м/с2.

 

Приклад 2. Тіло кинуте з висоти 12 м під кутом 300 до горизонту з початковою швидкістю 12 м/с. Визначити тривалість польоту тіла до точок A і B (рис. 1.1), максимальну висоту, на яку піднімається тіло, і дальність польоту тіла. Опір повітря не враховувати.

Дано: H = 12 м; α = 300; 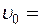12 м/с. Знайти: t А, tВ, h max, x max. Розв’язок. У системі координат, показаній на рис. 1.1, проекції початкової швидкості на осі координат дорівнюють: ; (1) ; (2) Координати тіла з часом змінюються Рис. 1.1.

відповідно до рівняння рівнозмінного (вздовж осі y) та рівномірного (вздовж осі x) руху

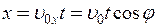; (3)

. (4)

Час підйому тіла знайдемо за умови, що в найвищій точці підйому тіла вертикальної складової його швидкості . Тоді з виразу (2) знайдемо час tп, що пройшов до підйому тіла на максимальну висоту

. (5)

Час спуску тіла від точки C до точки A дорівнює часу підйому, тому тривалість польоту тіла від точки O1 до точки A дорівнює

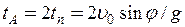. (6)

Максимальну висоту підйому знайдемо з рівняння (4), підставивши в нього час підйому з рівняння (5)

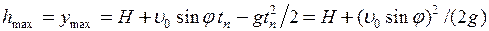. (7)

Час польоту тіла до точки В знайдемо, розв’язуючи квадратне рівняння (нефізичний розв’язок відкидається), отримане з виразу (4), у якому кінцева координата y (t) прирівнюється до нуля

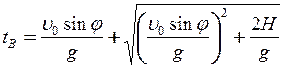. (8)

Дальність польоту знайдемо з рівняння (3), підставивши в нього час руху з рівняння (8)

. (9)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)