Обчислення. Приклад 8. Батарея складається з п’яти однакових гальванічних елементів, з’єднаних послід

Дж = 1,5·10^-3 Дж.

Відповідь: 1,5·10^-3 Дж.

Приклад 8. Батарея складається з п’яти однакових гальванічних елементів, з’єднаних послідовно. Кожен з цих елементів має ЕРС 1,4 В и внутрішній опір 0,3 Ом. При якому струмі корисна потужність батареї буде дорівнювати 8 Вт? Яку найбільшу корисну потужність може віддавати ця батарея?

Дано: = 1,4 В; r = 0,3 Ом; n =5; P_R = 8 Вт.

Знайти: I; P_R,max.

Розв’язок. При послідовному з’єднанні декількох гальванічних елементів їх можна замінити в розрахунках одним еквівалентним елементом. Внутрішній опір цього еквівалентного елемента дорівнює сумі внутрішніх опорів тих елементів, з яких він складений, а його ЕРС дорівнює алгебраїчній сумі ЕРС елементів. Це дозволяє записати закон Ома для даної задачі у такому вигляді

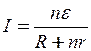. (1)

Корисна потужність, тобто потужність, що виділяється у навантаженні з опором R, дорівнює

. (2)

Якщо тепер виразити опір R з рівняння (2) і підставити результат у вираз (1), після нескладних перетворень можна одержати таке квадратне (по струму I) рівняння

. (3)

Рішення цього рівняння має стандартний вигляд

. (4)

Щоб знайти найбільшу корисну потужність, що віддається цією батареєю в зовнішнє коло, спочатку запишемо потужність як функцію опору навантаження, для чого підставимо вираз (1) у (2)

. (5)

Тепер скористаємося умовою екстремуму (максимуму) цієї функції, для чого знайдемо похідну від виразу (5) від змінної R, і дорівняємо її нуля

. (6)

З розв’язку цього рівняння випливає

. (7)

Підставляючи це рішення у вираз (5), одержимо остаточну формулу для обчислення максимальної потужності, що віддається даною батареєю в навантаження

. (8)

Поиск по сайту: