Обчислення. Приклад 12. Платформа у вигляді суцільного диску радіусом 1,5 м і масою 180 кг обертається біля вертикальної осі з частотою 10 об/хв

= 2,88 м/с².

Відповідь: a = 2,88 м/с².

Приклад 12. Платформа у вигляді суцільного диску радіусом 1,5 м і масою 180 кг обертається біля вертикальної осі з частотою 10 об/хв. У центрі платформи стоїть людина масою 60 кг. Яку лінійну швидкість щодо підлоги приміщення буде мати людина, якщо вона перейде на край платформи?

Дано: m ₁ = 180 кг; m ₂ = 60 кг; n ₁ = 10 об/хв = 1/6 об/с; R = 1,5 м;
r = 0.

Знайти: .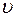

Розв’язок. Відповідно до умови задачі момент зовнішніх сил відносно осі обертання, що збігається з геометричною віссю платформи, можна вважати рівним нулю. За цієї умови діє закон збереження моменту імпульсу системи «платформа – людина»

. (1)

Тут L і – відповідно моменти імпульсу системи у вихідному й у кінцевому станах, для яких можна записати такі вирази

; (2)

. (3)

У цих виразах прийнято такі позначення: J ₁ і J ₂ – моменти інерції платформи і людини у початковому стані; і 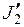– у кінцевому стані, відповідно; і – кутова швидкість обертання платформи у початковому й у кінцевому станах.

Кутову швидкість можна виразити через частоту обертання n, а величину пов’язати з пошукуваною кінцевою лінійною швидкістю людини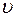

. (4)

. (5)

Зауважимо, що, відповідно до умови задачі, момент інерції платформи не змінюється, а для моменту інерції людини застосовною, є формула моменту інерції матеріальної точки

; (6)

; (7 a)

(7 б)

Тепер можна підставити вираження (2) і (3) у (1), використовуючи (4), (6) і (7). В результаті, приймаючи до уваги, що r = 0, а , можна одержати

. (8)

Остаточну формулу одержимо, підставляючи отриманий вираз у вираз (5)

. (9)

Поиск по сайту: