 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Операции над графами
Объединением графов G1=(A, Г1(А)) и G2=(В, Г2(В)) называется граф G=G1ÈG2= 
.
Пересечением графов G1=(A, Г1(А)) и G2=(В, Г2(В)) называется граф G=G1ÇG2= 
.
Пример. Для графов G1 и G 2, изображенных на рис. 2.13, найти графы G1ÈG2 и G1ÇG2.
Решение. A={x1, x2, x3, x4}; Г1(x1)={x2}; Г1(х2)={x3, x4}; Г1(х3)={x4}; Г1(х4)={x1}. B={x1, x2, x3, x4}; Г2(х1)={x3}; Г2(х2)={x1, x3}; Г2(х3)=Æ; Г2(х4)={x1, x3}.
Находим объединение графов G1 и G2 (рис. 2.14): AÈB={x1, x2, x3, x4}; Г1(х1)ÈГ2(х1)={x2, x3}; Г1(х2)ÈГ2(х2)={x1, x3, x4}; Г1(х3)ÈГ2(х3)={x4}; Г1(х4)ÈГ2(х4)={x1, x3}.
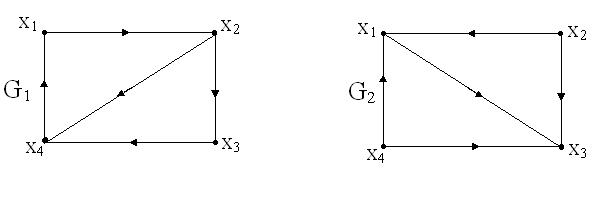Рис. 2.13
Находим пересечение графов G1 и G2 (рис. 2.14): AÇB={x1, x2, x3, x4}; Г1(х1)ÇГ2(х1)=Æ; Г1(х2)ÇГ2(х2)={x3}; Г1(х3)ÇГ2(х3)=Æ; Г1(х4)ÇГ2(х4)={x1}.
Рис.2.14
Декартовым произведением графов G1=(A, Г1(А)) и G2=(В, Г2(В)) называется граф G=G1´G2= 
.
Пример. Для графов G1 и G 2, изображенных на рис. 2.15, найти граф G1´G2 .
Рис. 2.15
Решение. A={X1, X2}, Г(Х1)={X2}, Г(X2)={X1};
B={Y1, Y2, Y3}, Г(Y1)={Y2}, Г(Y2)={Y3}, Г(Y3)={Y1, Y2}.
A´B={(X1, Y1), (X1, Y2), (X1, Y3), (X2, Y1), (X2, Y2), (X2, Y3)};
Г[(X1, Y1)]=Г(Х1)´Г(Y1)={(X2, Y2)}; Г[(X1, Y2)]=Г(Х1)´Г(Y2)={(X2, Y3)}; Г[(X1, Y3)] = Г(Х1)´Г(Y3)={(X2, Y1), (X2, Y2)}; Г[(X2, Y1)]=Г(Х2)´Г(Y1)= {(X1, Y2)}; Г[(X2, Y2)] = Г(X2)´Г(Y2)={(X1, Y3)}; Г[(X2, Y3)]=Г(X2)´Г(Y3)= {(X1, Y1), (X1, Y2)}.
В результате получаем граф, вид которого представлен на рис. 2.16.
Рис. 2.16.
2.9. Определение путей экстремальной длины
2.9.1. Задача о кратчайшем пути между двумя вершинами (ориентированного графа
Каждой дуге графа G(X, V) ставиться в соответствие неотрицательное число - l(V) - длина его дуги. Требуется для двух фиксированных вершин Х0, Хn найти кратчайший путь, их соединяющий. Если под длиной дуги l(Xi, Xj) понимать стоимость перевозки груза из пункта Xi в пункт Xj, то содержание задачи составит определение пути из Х0 в Хn, при котором затраты на перевозки минимальны
2.18
Данная задача предполагает, во-первых, определение длины кратчайшего пути, во-вторых, определение самого пути минимальной длины.
Алгоритм решения этой задачи позволяет определить кратчайший путь и его длину за конечное число шагов. Каждая вершина графа получает некоторую числовую метку на первом шаге. Затем метки вершин, вообще говоря, могут меняться, становясь на некотором шаге постоянным числом. Установившаяся метка данной вершины есть кратчайшее расстояние от этой вершины до вершины Х0. Если пути, соединяющего вершины Х0 и Хn не существуют, считают длину кратчайшего расстояния между ними +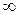 
Алгоритм состоит в выполнении следующих операций:
Шаг 1. Проставить следующие метки: для вершины Х0 - метку 
. Для любой другой вершины Xi, - метку 
Шаг 2. Найти на графе такую дугу (Xi, Xj), для которой
2.19
Разность 
считать равной 0. Если такая дуга найдется, то изменить метку вершины Хj на
2.20
Если такой дуги нет, то пути, соединяющего Х0 и Хn не существует.
Шаг 3. Повторять шаг 2 до тех пор, пока метки вершин не перестанут меняться.
Установившиеся метки обозначим 
Может быть два случая: 1) 
. Это значит, что пути, соединяющего Х0 и Хn не существует. 2) 
- конечное число. Оно равно кратчайшему расстоянию между Х0 и Хn.
Сам путь минимальной длины получим, отмечая вершины, по которым достигается минимум.
На графе-сети между входом и выходом графа путь минимальной длины всегда существует. Его можно определить за один шаг, если пользоваться формулой:
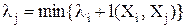2.21
Пример. Найти кратчайший путь между вершинами Х0 иX5. Длины дуг заданы на графе (рис. 2.17).
Рис. 2.17.
Решение. Имеем ориентированный граф без циклов, имеющий одну вершину Х0 без входящих дуг - вход графа, и одну вершинуХ5без выходящих дуг - выход графа. Такой граф есть граф-сеть.
Следуя алгоритму, обозначим 
Далее меняем метки всех вершин, кроме Х0. Смысл метки 
-некоторое расстояние от вершины Хi, до Х0. Поэтому метка вершины Х0 не меняется.
Для вершины X1: 
Поэтому меняем метку вершины X1 на
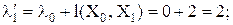Х0
Справа отметим вершину, из которой пришли в вершину X1. Аналогично для вершины Х2: 
Х0
В вершину Х3 ведут два пути: из вершины Х0 и из 'вершины X1. Поэтому используем формулу 2.21:
Х0
Справа обозначим вершину, по которой достигается минимум.
Аналогично для вершины Х4и Х5 получаем:
Х1
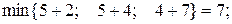Х4
Полученное значение 
= 5 есть длина минимального пути из Х0в Х5. Сам путь получим, проходя по отмеченным вершинам из Х5 в Х0: Х5, Х4, X1, Х0, т.е. 
= {Х0, X1, Х4, Х5} -искомый путь, а его длина 1() = 5.
Задача может иметь не единственное решение.
2.9.2 Задача о нахождении пути максимальной длины между двумя фиксированными вершинами ориентированного графа
Сетевое планирование.
Постановка задачи и ее решение аналогичны предыдущей задаче. Алгоритм решения задачи следующий:
Шаг 1. Проставить метки: для вершин Х0 = 0, для любой другой вершины Xi метку 
Шаг 2. Найти на графе такую дугу (Xi, Xj), для которой 
Изменить метку вершины Xj на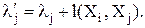 
Шаг 3. Повторять шаг 2 до тех пор, пока метки вершин не перестанут меняться.
На графе-сети получим решение за один шаг, если будем пользоваться формулой
2.22
Определим путь максимальной длины и его длину для условия предыдущей задачи.
Следуя алгоритму, полагаем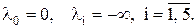 
Так как 
, то меняем метку вершины X1 на метку
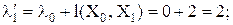Х0
Аналогично, для вершины X2:
Х0
Для определения метки вершины Х3 применяем формулу 2.22:
Х1
Справа отмечаем вершину, по которой достигается максимум.
Для вершины Х4 и Х5 получаем:
Х3
= 
Х4
Длина максимального пути из вершины Х0 в вершину Х5 
=14. Сам путь получим, просматривая отмеченные вершины: = {Х0, X1, Х3, Х4, X5}.
Путь максимальной длины - критический путь, его длина совпадает с критическим временем завершения проекта, представленного графом-сетью, т.е. с критическим временем. Вершина Х0 - событие, состоящее в начале всего проекта, т.е. всех работ, представленных на графе дугами; Xn - событие, состоящее в окончании всех работ, всего проекта. Другие вершины X1,..., Xn-1 - события, состоящие в начале одних и окончании других работ. Дуги графа - работы, составляющие проект. Последовательность выполнения работ - содержание проекта, представлено графом-сетью. Длина дуги - продолжительность выполнения данной работы. Скорейшее время завершения всего проекта совпадает с длиной пути максимальной длины из Х0 в Хn и называется критическим временем. Работы, составляющие критический путь не допускают запаздывания по времени.
Так, граф (рис. 2.18) может рассматриваться как некоторый проект, состоящий из девяти работ, заданных таблицей:
| Виды работ | Какие работы следуют за перечисленными | Продолжительность работ |
| 2,3 | ||
| 6,7 | ||
| 6,7 | ||
| - | ||
| - | ||
| - |
Поиск по сайту: