АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Счётные и несчётные множества

Читайте также:
  1. Бинарные соответствия между множествами.
  2. Вопрос. Множества и операции над ними
  3. Выпуклые множества
  4. Выпуклые множества и выпуклые функции.
  5. Выпуклые множества, свойства выпуклых множеств
  6. Выпуклые множества.
  7. Дополнение множества
  8. Если для множества Е выполняются все вышеперечисленные условия, то множество Е называют линейным пространством.
  9. Задача о доставке (покрытии множества)
  10. Использование множества таблиц в одном запросе. Связывание таблиц.оператора SELECT, в предложении FROM допускается указание нескольких таблиц.
  11. Каким термином характеризуется философское учение, признающее существование множества субстанций?
  12. Любая система может быть рассмотрена как множество, но не любое множество может быть рассмотрено как система. Важно понимать, что понятие множества отличается от понятия системы

 

Простейшими среди бесконечных множеств является множество натуральных чисел.

Определение: Множество называется счётным, если элементы множества биективно сопоставлены со множеством натуральных чисел.

Приведём примеры счётных множеств.

Пример 1. Имеем множество всех целых чисел. Установим соответствие между всеми натуральными числами по схеме:

0, -1, 1, -2, 2, -3, 3…,

1, 2, 3, 4, 5, 6, 7…,

Вообще, для n ³ 0 сопоставим нечётное число 2n+1, а отрицательному n < 0 – чётное число 2|n|, и тогда получим:

n «2n+1 при n ³ 0; n «2|n| при n < 0.

Пример 2. Множество 2, 4, 8, 16… 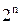… счетно.

Действительно, в данном случае имеем множество степеней числа 2. Здесь каждому числу 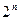соответствует число n.

Пример 4. Множест-во всех рациональных чисел – счетно. Известно, что рациональное число можно представить в виде дроби r=q/p, где q и p – любые целые числа. Для того чтобы убедиться в том, что множество рациональ-ных чисел счетно, представим все  
Итак, если бесконечное множество оказывается возможным привести во взаимно однозначное соответстивие с натуральным рядом чисел, то такое множество называют счетным.1 Если бесконечное множество невозможно привести во взаимно однозначное соответсвие с натуральным рядом чисел, то его называют несчетным.

………….

 

………….

 

………….

 

…………

       
   


..... …………

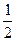
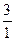
множество рациональных чисел в виде таблицы, в которую занесем несократимые дроби. Обходя таблицу по направлению стрелок, приходим к последовательности

1, 2, 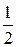, , 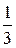, 3, 4, , , , , , , ,…..,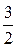

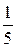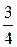позволяющей занумеровать все эти числа

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)