АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Универсальное множество

Читайте также:
  1. А) Безграничное конкретное множество; b) равенство (неравенство).
  2. Белки выполняют в клетке множество функций: ферментативную, транспортную, структурную, защитную и другие. Без белков жизнь клетки невозможна.
  3. Бюджетное множество
  4. Вирусы вызывают множество болезней
  5. Г. – уничтожен дом и библиотека М. Грушевского, в которой было множество материалов, указывающих на нынешнюю Украину, как первоначального основателя Руси.
  6. Глава 7. Эгнонационапьное и универсальное в современной обыденной культуре
  7. Глава III. Великий переворот, или множество «рук» машины (30-е годы XVIII в. – середина XIX в.)
  8. Двойственно допустимое базисное множество
  9. Для описания множественного типа используется словосочетание set of (множество из...).
  10. Допустимое базисное множество
  11. Если для множества Е выполняются все вышеперечисленные условия, то множество Е называют линейным пространством.
  12. Квакают ученые множество лет

Если в некотором рассмотрении участвуют только подмножества некоторого фиксированного множеств I, то это самое большое множество называют универсальным (или полным) множеством, или - универсум.

В различных конкретных случаях роль универсального множества играют различные множества. Так, при рассмотрении студентов института универсальным (полным) множеством является вся совокупность студентов. Отдельные группы (факультеты) можно рассматривать как подмножества. В некоторых случаях универсальным множеством может являться и отдельная группа, в которой имеют место свои подмножества (отличники; студенты, проживающие в общежитии; юноши; девушки и т.п.).

Вполне очевидно, что для универсального множества справедливы следующие соотношения:

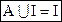и 1.19

Универсальное множество удобно изображать графически в виде множества точек прямоугольника. Различные области внутри прямоугольника будут означать различные подмножества универсального множества. Изображение множества в виде областей в прямоугольнике, представляющем универсальное множество, называют диаграммой Эйлера-Венна.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)