АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Объединение любого конечного или счетного множества счетных множеств есть снова счетное множество

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. I . Экономически обоснованные страховые тарифы.
  3. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  4. III. Принципы конечного результата
  5. III. Принципы конечного результата.
  6. V. Множественные волнообразные линии
  7. ZOOSN (ПРИК.Основания пунктов приказов)
  8. ZOSNSP (ЗП.Основания начислений Параметры)
  9. А) Безграничное конкретное множество; b) равенство (неравенство).
  10. а) на основании договора юридическому или физическому лицу
  11. А) процесс выделения на электродах веществ, входящих в состав электролита Б) объединение ионов разных
  12. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство

Доказательство. Пусть А1, А2, … - счетные множества. Можно считать, что они попарно не пересекаются.2 Все элементы множеств А1, А2, … можно записать в виде следующей бесконечной таблицы:

 

      а11 а12 а13 а14 ….            
      а21 а22 а23 а24 ….            
      а31 а32 а33 а34 ….            
      … … … … …            

где в первой строке стоят элементы множества А1, во второй – элементы множества А2 и т. д. Занумеруем все эти элементы по диагоналям, т.е. за первый элемент примем а11, за второй а12, за третий а21 и т.д., двигаясь в порядке, указанном стрелками на следующей таблице:

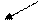
    а11 а12 а13 а14 ….    
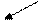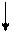
    а21 а22 а23 а24 ….    
    а31 а32 а33 а34 ….    
      … … … … …    

Ясно, что при этом каждый элемент каждого из множеств получит определенный номер, т.е. будет установлено взаимно однозначное соответствие между всеми элементами всех множеств А1, А2, … и всеми натуральными числами. Утверждение доказано.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)