Понятие мощности множества

Если эквивалентны два конечных множества, то они состоят из одного и того же числа элементов. Если же эквивалентные между собой множества M и N произвольны, то говорят что M и N имеют одинаковую мощность. Т.о. мощность это общее, что есть у любых двух эквивалентных между собой множеств. Для конечных множеств понятие мощности совпадает с принятым понятием числа элементов множества, и обозначается так:

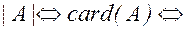m(A).

Мощность эквивалентных множеству всех действительных чисел отрезка [0,1] называют мощностью континуума.

Для мощности конечных множеств, т.е. для натуральных чисел кроме понятия равенства имеются также понятия “больше” и ”меньше”

Пусть А и В произвольных множества, а m(А) и m(В) – их мощности. Тогда логически возможны следующие случаи:

1. А эквивалентно некоторой части множества В, и В эквивалентно некоторой части множества А.

2. А содержит некоторую часть, эквивалентную В, но в В нет части, эквивалентной А.

3. В содержит некоторую часть, эквивалентную А, но в А нет части, эквивалентной В.

4. Ни в одном из этих множеств нет части, эквивалентной другому.

В первом случае множества А и В в силу теоремы Кантора-Бернштейна эквивалентные между собой, т.е. m(А)=m(В). Во втором случае естественно считать, что m(А)>m(В), а в третьем, что m(А)<m(В). В четвертом случае нам пришлось бы считать, что мощности множеств А и В несравнимы между собой. Но на самом деле этот случай невозможен.

Итак, любые два множества А и В либо эквивалентны между собой (и тогда m(А)=m(В)), либо удовлетворяют одному из двух соотношений: m(А)<m(В) или m(А)>(В).

Поиск по сайту: