Проекция множества

Операция проектирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.

Как было уже показано в предыдущем параграфе, проекцией кортежа Х=(х₁, х₂,…х_n) на i-ю ось называется его i-тая координата (компонента) х_i и обозначаемая Пр_ix=x_i. Проекцией кортежа на оси с номерами i₁, i₂, … i_n называется кортеж длины n (напомним, что длиной кортежа называется число его координат). Обозначается эта проекция . Пусть М – множество кортежей длины n. тогда проекцией множества М на i-ю ось называется множество проекций всех кортежей из М на i-ю ось и обозначается . Аналогично определяется проекция множества М на несколько осей: . В частности, если М=А₁´А₂´¼А_n, то .

Пример 1. Проекция точки плоскости на первую ось – ее абсцисса, на вторую ось – ее ордината.

Пример 2. М={(a, b, d); (c, b, d); (d, b, b)}.

Проекция этого множества Пр₁М={a, c, d}; Пр₂M={b}; Пр_2,3M={(b, d), (b, b)}.

1.10 Соответствия

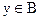Рассмотрим два множества А и В. Элементы этих двух множеств могут каким-либо образом сопоставляться друг с другом, образуя пары (x, y). Если способ такого сопоставления определен, т.е. для каждого элемента указан элемент , с которым сопоставляется элемент x, то говорят, что между множествами А и В установлено соответствие. При этом не обязательно, чтобы в сопоставлении участвовали все элементы множества А и В. Для того, чтобы задать соответствие, необходимо указать:

· множество А, элементы которого сопоставляются с элементами другого множества;

· множество В, с элементами которого сопоставляются элементы первого множества;

· множество , определяющее закон, в соответствии с которым осуществляется соответствие, т.е. перечисляющее все пары x и y. Таким образом, соответствие, обозначаемое, например, q, представляет собой тройку множеств:

q=(A, B, P); P=A´B.

В этом выражении 1-ю компоненту А называют областью отправления соответствия, 2-ю компоненту В – областью прибытия соответствия, 3-ю компоненту P – графиком соответствия.

Кроме рассмотренных множеств А, В, Р с каждым соответствием неразрывно связаны еще два множества: множество Пр₁Р, называемое областью определения соответствия, и в которое входят элементы множества А, участвующие в сопоставлении, и множество Пр₂Р, называемое областью значений соответствия, в которое входят элементы множества В, участвующие в сопоставлении. Если Пр₁Р=А, то соответствие называется всюду определенным, в противном случае – частично определенным. Если Пр₂Р=В, то соответствие называется сюръективным.

Множество всех уÎВ, соответствующих элементу хÎА, называется образом х в В при соответствии Р. Множество всех х, которым соответствует у, называется прообразом у в А при соответствии Р. Короче, образ х есть Р(х)={y | (x, y) Î P}, а прообразом элемента уÎВ (обозначается Р^-1(у)) является Р^-1(у)={x | (x, y) Î P}.

Если , то говорят, что элементу y соответствует элемент х при соответствии Р. Геометрически это удобно изображать стрелкой, направленной от х к у.

Пример: A={3, 4}; B={2, 5}. P=A´B={(3, 2), (3, 5), (4, 2), (4, 5)}.

Это множество дает возможность получить соответствия:

Р₁={(3, 2)}; P₂={(3, 2), (3,5)}; P₃={(3, 2), (3, 5), (4, 2)}.

Если D Пр₁Р, то образом множества D называется объединение образов всех элементов из D. Аналогично определяется прообраз множества SÌ В для любого SÌПр₂Р.

Соответствие Р называется функциональным (или однозначным), если образом любого элемента Пр₁Р является единственный элемент из Пр₂Р. Заметим, что здесь не говорится о том, что различные элементы из Пр₁Р должны иметь различные образы из Пр₂Р.

Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества В имеет не более одного прообраза в А.

Соответствие Р между А и В называется взаимнооднозначным, если оно всюду определено, сюръективно, функционально и инъективно.

Пример 1. Англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Это соответствие не является функциональным, так как одному английскому слову, как правило, ставится в соответствие несколько русских слов. Кроме того, оно практически никогда не является полностью определенным: всегда можно найти английское слово, не содержащееся в данном словаре. Областью отправления является множество всех английских слов, областью прибытия – множество всех русских слов. Область определения (значений) является подмножеством области отправления (прибытия).

Пример 2. Круг Р радиуса 1 с центром в точке (3, 2) {(x, y) | (x –3)²+(y-2)² £1} задает соответствие между R и R. Образом числа 4 при этом соответствии является число 2, образом числа 3 – отрезок [1, 3] оси ординат; этот же отрезок [1, 3] является образом отрезка [2, 4] оси абсцисс, который в свою очередь служит прообразом числа 2 (См. Рис.1.8).

Рис. 1.8

Данное соответствие не является функциональным. Примером функционального соответствия является дуга АВС.

Пример 3. Различные виды кодирования – кодирование букв азбукой Морзе, представление чисел в различных системах счисления, секретные шифры и т.п. – являются соответствиями между кодируемыми объектами и присваемыми им кодами. Эти соответствия, как правило, обладают всеми свойствами взаимно однозначного соответствия, кроме, быть может, одного – сюръективности.

Пример 4. В цехе имеется 3 специализированных станка Ст₁, Ст₂, Ст₃. Станок Ст₂ не работает. Штат содержит три оператора, обслуживающие эти станки – О₁, О₂, и О₃. Причем, О₃ болен (или в отпуске и т.п.) В этом случае распределение операторов по станкам можно выразить соответствием:

Геометрическая интерпретация имеет вид:

О₁ О₂ О₃

Ст₁ Ст₂ Ст₃

Как видно, здесь областью определения соответствия является множество Пр₁Р= {О₁, О₂} ¹ А. Следовательно, соответствие является частично определенным. Областью значений соответствий является множество Пр₂Р = {Ст₁, Ст₃} ¹В и, следовательно, соответствие является несюръективным. Вполне очевидно, что соответствие не является функциональным, так как образом О₁ из А являются два элемента в В - Ст₁ и Ст₃. Соответствие является и неинъективным, т.к. элемент Ст₁ имеет два прообраза - О₁ и О₂.

Поиск по сайту: