Отношения. Важным частным случаем отображения является случай, когда множества A и B совпадают

Важным частным случаем отображения является случай, когда множества A и B совпадают. При этом отображение R: A®A будет представлять собой отображение множества A в самого себя и будет определяться парой (A, R), где RÍA². В этом случае для обозначения данного отображения используется термин отношение и вводят специальную символику. Пусть отображение (A, R) является отношением. Рассмотрим элемент (a,b) ÎRÍA². Говорят, что элемент a находится в отношении R к элементу b и записывают это в виде aRb

Подмножество RÌA₁´A₂´…´A_n называется n-местным отношением между А₁, А₂, …..А_n (или просто на А, если А₁=А₂=….=А_n=А). Если n=1, то R называется унарным отношением. В этом случае R есть просто подмножество множества А, RÌА. Если n=2, то R называется бинарным отношением между А₁ и А₂, RÌА₁´А₂. Если n=3, то R называется тернарным отношением, А₂, RÌА₁´А₂´А₃. Говорят, что (а₁, а₂, …а_n) находятся в отношении R, если упорядоченная n-ка а₁, а₂, …а_n)ÎR. Одноместные отношения называются признаками: а обладает признаком R.

Наиболее часто встречаются бинарные отношения. Если R есть некоторое бинарное отношение, то запись (х, у)ÎR и xRy –взаимозаменяемы.

Пример 1. Множество {(2, 4), (7, 3), (3, 3), (2, 1)}, будучи множеством упорядоченных пар натуральных чисел, есть бинарное отношение на N, где N – множество натуральных чисел.

Пример 2. Отношение “меньше чем” для целых чисел есть множество {(x, y)| для целых чисел х и у найдется такое положительное число z, что x+z=y}. Если это отношение выразить символически обычным образом, то предложения “4<9” и “(4, 9)Î <” будут синонимичны (здесь знаком “<” обозначено отношение “меньше чем”).

Пример 3. Операция сложения в множестве целых чисел z: выражение k=m + n можно записать в форме утверждения (k, m, n)Î +, т.е. k есть сумма целых чисел m и n. Это отношение является тернарным отношением.

Для бинарных отношений, являющихся как и соответствия, подмножествами прямых произведений, аналогично соответствиям вводятся понятия области определения, области значений, проекции на множества (оси) и т.п. Например, область определения отношения R – это множество первых координат из R, а область значений R – множество вторых координат элементов из R. Например, областью определения для отношения материнства служит множество всех матерей, в то время как областью значений этого отношения – множество всех людей.

Пусть дано отношение R на А. Для любого подмножества А₁ÎА естественно определяется отношение 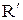, называемое сужением R на А₁, которое получается из R удалением всех пар, содержащих элементы, не принадлежащие А₁. Другими словами, .

Поиск по сайту: