Функция времени

В основе понятия функции времени лежит множество ТÍR с элементами t, называемое множеством моментов времени. Время обладает направленностью. Если и ÎT, и < , то момент предшествует моменту , т.е. Т – упорядоченное множество.

Функция времени определяет отображение f множества моментов времени Т на множество вещественных чисел R: f: Т®R. Элементами f будут пары (t, x), обозначаемые x(t), где tÎ T, хÎR. Каждая такая пара определяет значение функции в момент t и называется событием или мгновенным значением функции. Дальнейшее уточнение функций времени связано с уточнением ее области определения, т.е. вида множества Т. Если T=R, т.е. t принимает любые вещественные значения от -¥ до +¥, то x(t) называют функцией с непрерывным временем. Например, .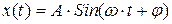

В практике часто используют сужение x(t) на ограниченный интервал времени t₁<t£t₂, который обычно считают полузакрытым и обозначают (t₁, t₂]. Полузакрытые интервалы удобны тем, что допускают последовательное соглашение друг с другом.

Сужение функции x(t), заданной на интервале на интервал (t₁, t₂] называют отрезком функции x(t) и обозначают , т.е. .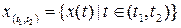

Если множество Т представляет собой множество натуральных чисел, то говорят о функции с дискретным временем. В этом случае элементы множества Т обозначают через n, так что пара (n, x), обозначаемое также x[n] или x_n определяет значение функции в момент n.

Поиск по сайту: