 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Отношение порядка и отношение эквивалентности на графе
Граф дает удобное геометрическое представление отношений на множестве, поэтому теория графов и теория отношений на множестве взаимно дополняют друг друга.
На графе G=(X, Г) введено отношение порядка, если для любых двух вершин (х и y), удовлетворяющих условию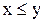 
, существует путь из х в у. В этом случае говорят, что вершина х предшествует вершине у, или что вершина у следует за вершиной х.
Данное определение отражает на графе все свойства отношения порядка.
Рефлексивность. Условие
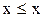истинно 2.12
означает эквивалентность вершины самой себе, т.е. условие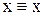 
. Однако при желании это условие можно рассматривать как наличие пути из х в х, т.е. как петлю в вершине х (рис.2.11 а).
Транзитивность. Условие
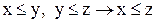2.13
означает, что вершины х, у, z последовательно встречаются на одном и том же пути (рис. 2.11 б).
Антисимметричность.
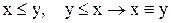2.14
Левая часть этого выражения говорит о том, что существует путь из х в у, а так же существует путь из у в х. Но это означает, что в графе имеется контур, на котором лежат вершины х и у (рис.2.11 в).
Из правой части условия 2.14 вытекает, что вершины, лежащие на одном и том же контуре, являются эквивалентными. Будем рассматривать этот вывод как определение эквивалентности на графе и покажем, что такое определение удовлетворяет всем трем условиям отношения эквивалентности. Условия рефлексивности 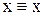и симметрии 
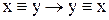являются очевидными и вытекают из данного выше определения эквивалентности. Условие транзитивности 
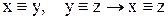также является очевидным, так как говорит о том, что если в графе имеется контур с вершинами х и у, а так же контур с вершинами у и z, то имеется и контур, на котором лежат вершины х и z (рис.2.11 в).
Таким образом, отношение порядка совместно с отношением эквивалентности определяет некоторый граф.
На графе может быть так же введено отношение строгого порядка. В этом случае для любых двух вершин (х и у), удовлетворяющих условию x<y, существует путь, идущий из х в у. Условие транзитивности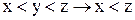 
означает, как и в предыдущем случае, что вершины х, у и z встречаются последовательно на одном и том же пути. Условие антирефлексивности (х<x ложно) говорит об отсутствии петель на графе, а условие несимметрии (x<y, y<x взаимоисключается) говорит об отсутствии контуров.
Таким образом, отношение строгого порядка определяет граф без контуров.
Поиск по сайту: