 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Операция удаления ребра
Пусть G=(V,E) – граф, и 
- некоторое его ребро. Граф G1 = G-e получен из графа G в результате удаления ребра е, т.е. 
. Следовательно, концы ребра е не удаляются из множества V. Также вполне очевидно, что 
. Действительно, поскольку имеет место тождество 
, то имеем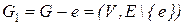 
.
Следовательно, если выполняется операция удаления сразу нескольких ребер (дуг), то это можно делать в произвольной очередности, т.к. результат, как мы определили, не зависит от очередности удаления ребер (дуг) в графе.
Рис. 2.5
На рис. 2.5 приведен пример последовательного удаления 2-х ребер: (1,2) и (4,5).
Поиск по сайту: