Пример. Пусть даны множества А={a, b, c, d, e, f, g, h} и В = {1, 2, 3, 4, 5, 6, 7, 8}

Пусть даны множества А={a, b, c, d, e, f, g, h} и В = {1, 2, 3, 4, 5, 6, 7, 8}

Тогда есть множество обозначений шахматной доски.

Мощность произведения конечных множеств равна произведению мощностей этих множеств, т.е. | | = |A|×|B|.

Операция прямого произведения легко распространяется и на большее число множеств..Прямым произведением множеств А₁, А₂, … А_n называют множество, обозначаемое А₁´А₂´….´А_n = {(a₁,a₂,…a_n) | a_i Î А_i }.

Вполне очевидно, что | А₁´А₂´….´А_n | = |A₁|×|A₂|×…×|A_n|

Из определения прямого произведения множеств видно, что прямое произведение некоммутативано, т.е. А´В¹В´А.

Пусть X и Y – отрезки вещественной оси. Прямое произведение X´Y является прямоугольником, каждая точка которого определяется координатами X и Y. (Рис. 1.7)

J

Рис.1.7

Частным случаем операции прямого произведения является понятие степени множества: (k –целое, >0). Специально определено, что М¹=М; М⁰=(). Если R – множество вещественных чисел, то R²=R´R представляет собой вещественную плоскость, а R³=R´R´R – трехмерное вещественное пространство.

Свойства прямого произведения. Прямое произведение дистрибутивно относительно объединения и пересечения, т.е

1. 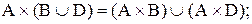1.35

1.36

2. 1.37

1.38

Поиск по сайту: