АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Характеристики графов

Читайте также:
  1. Cущностные характеристики техники
  2. I. Схема характеристики.
  3. А выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
  4. Акустические колебания, их классификация, характеристики, вредное влияние на организм человека, нормирование.
  5. Амплитудно частотные характеристики различных приборов, измеряющих частоту электрических сигналов.
  6. Амплітудна і фазова частотні характеристики
  7. Антикризисные характеристики управления персоналом
  8. Антропометричні характеристики людини
  9. Антропометричні характеристики людини.
  10. АРХ 18. Приведите основные качественные характеристики промышленных зданий павильонного типа. Сопоставьте здания павильонного типа со зданиями сплошной застройки.
  11. БАЗОВЫЕ ХАРАКТЕРИСТИКИ ОБЩЕСТВА
  12. Бюджетна система України: основні характеристики

 

Решение многих технических задач методами теории графов сводится к определению соответствующих характеристик графов. Из множества характеристик отметим следующие.

Цикломатическое число. Пусть G – неориентированный граф, имеющий n вершин, m ребер и k компонент связности. Цикломатическим числом графа G называют число

2.15

Физический смысл цикломатического числа заключается в том, что его значение определяет наибольшее число независимых циклов в графе. При расчете электрических цепей цикломатическим числом можно пользоваться для определения числа независимых контуров.

Хроматическое число. Граф G называют n-хроматическим (n-натуральное число), если его вершины можно раскрасить n различными цветами так, чтобы никакие две смежные вершины не были раскрашены одинаково. Наименьшее число n, при котором граф является n-хроматическим, называют хроматическим числом графа и обозначают .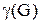

Если 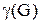=2, то граф называют бихроматическим. Необходимым и достаточным условием того, чтобы граф был бихроматическим, является отсутствие в нем циклов нечетной длины. Хроматическое число играет важную роль при решении задачи наиболее экономичного использования ячеек памяти при программировании. Однако его определение, за исключением случая бихроматического графа, представляет собой довольно трудную задачу, требующую нередко применения ЭВМ.

Множество внутренней устойчивости. Множество графа 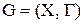называют внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для любого имеет место .

Внутренне устойчивое множество Si называется максимальным, если в графе G не существует такого другого внутренне устойчивого множества Sk, что .

Пример. Для графа, приведенного на рис. 2.11, множества S1={x1, x3}, S2={x2, x4}, S3={x2, x6}, S4={x2, x4, x6} являются внутренне устойчивыми. Из них множества S1 и S4 – максимальные, а множества S2 и S3 не являются таковыми, так как и .

Рис. 2.11

 

Очевидно, что число элементов в разных максимальных внутренне устойчивых множеств не обязательно одинаковое.

Если D – семейство всех внутренне устойчивых множеств графа G, то число

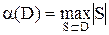2.16

называется числом внутренней устойчивости графа G, а множество S*, на котором достигается этот максимум, называется наибольшим независимым множеством.

Множество внешней устойчивости. Множество 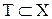графа G=(X, Г) называют внешне устойчивым, если любая вершина, не принадлежащая T, соединена дугами с вершинами из T, т.е. для любого имеет место .

Внешне устойчивое множество Ti называют минимальным, если в G не существует другого внешне устойчивого множества Tk, так что

Пример. Для графа, изображенного на рис. 2.12, множества Т1={X1, X4, X6}, T2={X1, X4}, T3={X3, X5, X6} являются внешне устойчивыми. Множества T2 и T3 минимальные, а Т1 не является минимальным, так как внешне устойчивое множество .

Рис.2.12.

 

В графе может быть несколько минимальных внешне устойчивых множеств и в общем случае они не содержат одинаковое число вершин.

Если R – семейство внешне устойчивых множеств графа, то число

2.17

называется числом внешней устойчивости графа, а множество Т*, на котором достигается минимум, называется наименьшим внешне устойчивым множеством.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)