Отношение порядка

Часто приходится сталкиваться с отношениями, которые определяют некоторый порядок расположения элементов множества. Т. е. во многих случаях можно расположить элементы множества А или группы элементов в некотором порядке или другими словами - ввести отношение порядка на множествах.

Различают отношение нестрогого и строгого порядка.

Отношением нестрогого порядка называют отношение, обладающее свойствами:

Ø х £ х истинно (рефлексивность);

Ø х £ у и у £ х Þ х=у (антисимметричность);

Ø х £ у и у £ z Þ х £ z (транзитивность).

Отношением строгого порядка называют отношение:

Ø x < x ложно (антирефлексивность);

Ø x < y и y < x взаимоисключается (несимметричность);

Ø x < y и y < z Þ x < z транзитивность.

Элементы а и b сравнимы по отношению порядка R, если выполняется условие аRb или bRa. Множество А, на котором задано отношение порядка R, называется полностью (линейно) упорядоченным, если любые два элемента А сравнимы, и частично упорядоченным в противном случае.

Пример 1. Отношения “£”, “³” являются отношением нестрогого порядка (или просто отношением порядка), а отношения “<”, “>” являются отношением строгого порядка. Оба отношения полностью (линейно) упорядочивают множества чисел N, Z, R.

Пример 2. Определим отношения “£” и “<” для n-элементных числовых кортежей следующим образом: (a₁, a₂, … a_n) £ (b₁, b₂, … b_n), если a₁£ b ₁, a₂£ b₂, … a_n£ b_n); (a₁, a₂, … a_n) < (b₁, b₂, … b_n) если (a₁, a₂, … a_n) £ (b₁, b₂, … b_n) и хотя бы для одной координаты выполнено условие a_i < b_i. Эти отношения определяют частичный порядок на множестве n-элементных кортежей (векторов) с числовыми координатами. Кортежи (5, 3, -2) < (5, 4, -2), a кортежи (5, 2, -3) и (5, 0, 0) не сравнимы.

Пример 3. Система подмножеств множества А отношением включения частично упорядочена. Например, {1, 2}Ì {1, 2, 3}, a {1, 2} и {1, 3, 4} не сравнимы.

Пример 4. Отношение подчиненности на предприятии задает строгий частичный порядок. В нем несравнимыми являются сотрудники разных подразделений.

Пример 5. Пусть дан алфавит А=(а, б, …) Отношением предшествования этот алфавит полностью упорядочивается. Отношение предшествования обозначается знаком “<” (a_i < a_j, если a_i предшествует a_j в списке букв алфавита). На основе отношения предшествования букв строится отношение предшествования слов, определяемое следующим образом:

Пусть даны слова a₁ = а₁₁, а₁₂, …а_1m, a₂ = a₂₁, a₂₂, … a_2m. Тогда a₁ < a₂ если и только если либо: 1). - некоторые слова, возможно пустые; - буквы); 2). 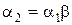, где b - непустое слово (Например, a₁ – слово “стол”, а a₂ – “столовая”, тогда b - слово “овая”). Это отношение задает полное упорядочение множества всех конечных слов в алфавите А, которое называется лексикографическим упорядочением слов. Заметим, что под словом здесь понимается любая последовательность букв, записанных рядом, возможно, пустая. Лексикографическое упорядочение дат от ранних к поздним требует следующей их записи: сначала год, потом месяц, затем число месяца. Например, 99.01.01.

На множестве А может задаваться несколько отношений R_i, iÎI, включая и эмпирические отношения и отношения операции. Примерами эмпирических отношений являются отношения доминирования, предпочтения, сравнения по любым признакам. Примерами отношений, задаваемых с помощью операций, являются алгебраические операции сложения, умножения и т. п.

Между элементами множества А имеет место доминирования, если эти элементы обладают свойствами:

Ø никакой элемент не может доминировать над самим собой, т.е. х>>х ложно (антирефлексивность);

Ø x>>y и y>>x взаимоисключается (несимметричность);

Ø транзитивность исключается.

Поиск по сайту: