Примеры

1. Пусть А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда

={1,2,4,5,7,8,12,16,17, 21,30}.

2. Пусть A={a,b,c,d}; B={a,d,e,f,g}. Тогда ={a,b,c,d,e,f,g}.

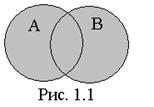Если множества А и В представить в виде точек, ограниченных окружностями А и В соответственно, то объединение множеств представляет собой закрашенную область, ограниченную обоими кругами, как это показано на рис. 1.1.

Понятие объединения множеств можно распространить и на большее число множеств. Пусть М={X₁, X₂,…. X_n} – совокупность n множеств X₁, X₂, … X_n, называемую системой множеств. Объединение этих множеств представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств системы М.

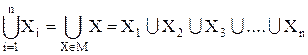1.7

Для объединения множеств справедливы коммутативный и ассоциативный законы:

; 1.8

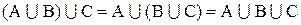. 1.9

Вполне очевидно, что 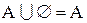. 1.10

Поиск по сайту: