КIНЕМАТИКА

Кiнематика — роздiл механiки, в якому вивчається рух тiл, не встановлюючи причин, що викликали цей рух. Сам термiн походить вiд грецького слова „кiнета”, що означає рух. За законами i залежностями, встановленими в кiнематицi, визначаються параметри польоту лiтальних апаратiв, виконуються розрахунки передач рухiв у рiзних авiацiйних механiзмах та iн.

1.1. Механiчний рух. Система вiдлiку

Механiчним рухом називається змiна положення тiла в просторi вiдносно iнших тiл. Це все свідчить, що механiчний рух є вiдносним. Дiйсно, будь-яке тiло може бути нерухомим вiдносно одних тiл i рухається вiдносно iнших. Разом з тим цей рух є абсолютним, оскiльки завжди можна вказати, таке тiло, вiдносно якого дане „нерухоме” тiло рухається, тобто абсолютно нерухомих тiл в природi не iснує. Отже, починаючи дослiджувати рух якогось тiла, слід визначити, вiдносно якого iншого тiла вiн буде розглядатися. Тiло, вiдносно якого розглядається рух, називається тiлом вiдлiку. Для математичного описування руху з тiлом вiдлiку необхiдно зв’язати систему координат. Як вiдомо, iснує багато рiзних систем координат (полярна, цилiндрична, сферична та iн.). Найбiльш поширеною є прямокутна декартова система координат.

Слiд звернути увагу, що iснують два види декартових систем:

права (рис. 1.1) та лiва (рис.1.2), якi розрiзняють за допомогою правила гвинта: якщо обертати ручку гвинта вiд додатнього кiнця осi ОХ до додатнього кiнця осi ОУ, то в правiй системi координат гвинт буде поступально рухатись у додатньому напрямку осi ОZ, а в лiвiй системi — у вiд’ємному напрямку. У фiзицi здебiльшого застосовується права система.

Перемiщення тiл вiдбувається з плином часу, тому для описування руху слід мати також годинник. Тiло вiдлiку, повязана з ним система координат та годинник становлять систему вiдлiку.

1.2. Способи описування руху матерiальноiї точки. Основна (пряма) задача кінематик

Траєкторiя — це уявна лiнiя, вздовж якої рухається матеріальна точка (рис. 1.3).

Шлях (∆S або S) — це довжина траєкторiї (рис. 1.3). Шлях — величина скалярна, в системi СІ вимiрюється в метрах (м).

Перемiщення ∆r — це найкоротша вiдстань мiж початковою i кiнцевою точками траєкторїi (рис. 1.4). Перемiщення — величина векторна, має напрямок вiд початковоїi до кiнцевої точки траєкторiї; в системi СІ вимiрюється в метрах.

У декартовiй системi координат положення матерiальної точки М може бути задане не тiльки трьома координатами (х, у, z), а й за допомогою радiуса-вектора. Радiус — вектором точки називається вектор, який проведено з початку координат у дану точку (рис. 1.5).

Радiус-вектор може бути записаний через його проекцiї 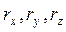на вiдповiднi координатнi осi:

(1.1)

та за модулем:

, (1.2)

де - одиничні вектори (орти) відповідних осей координат:

де

Оскільки формули (1.1) і (1.2) можуть бути записані ще й так:

, (1.3)

. (1.4)

У фізиці прийнято модуль будь-якого вектора позначати а.

Зрозумiло, що пiд час руху матерiальної точки‚ її радіус-вектор, шлях та координати з часом змiнюються. Вiдповiдно до цього в кiнематицi використовуються три способи описування руху:

— векторний, коли вiдоме рiвняння залежностi радіус-вектора точки вiд часу:

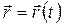(1.5)

— траєкторний, коли вiдоме рiвняння руху точки вздовж траєкторії:

(1.6)

— координатний, коли вiдомi рiвняння руху точки в декартових координатах:

х = х(t), у =у(t), z=z(t). (1.7)

Рiвняння (1.5), (1.6), (1.7) називаються кінематичними рiвняннями руху.

Основна (пряма) задача кiнематики полягає в тому, щоб за кiнематичними рiвняннями руху знайти положення матеріальної точки в просторi i кiнематичнi характеристики руху в будь-який момент часу.

1.3. Кiнематичнi характеристики поступального руху матерiальної точки