Кут повороту

Положення матерiальної точки пiд час руху по колу можна визначити кутом повороту . Як видно з рис. 1.11,а, кут повороту з центральним кутом, який вiдповiдає дузi , описанiй матерiальною точкою за час . Вимiрюється кут повороту в радiанах (рад) i є скалярною величиною. Один оберт точки по колу дорiвнює 2 , а при N обертах:

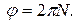(1.39)

Із геометрiї вiдомий зв’язок мiж довжиною дуги та кутом повороту:

(1.40)

де R— радiус кола. Для малих промiжкiв часу цей вираз матиме вигляд:

(1.41)

де - елементарний кут повороту. Для того, щоб показати i напрямок руху точки по колу, домовились елементарний кут повороту показувати як вектор , що вiдкладається вздовж осi обертання. Напрямок вектора визначається за правилом правого гвинта: вектор елементарного кута повороту збiгається за напрямком з поступальним рухом гвинта, ручка якого обертається в напрямку руху точки по колу (рис. 1.11,а). Такi „штучні” вектори називаються псевдовекторами.

Поиск по сайту: