АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Момент iнерції

Читайте также:
  1. Бумаге, подается не позднее, чем через один год с того момента,
  2. В начальный момент времени
  3. В понимании философии выделяют два основных момента: 1. Является ли философия наукой? 2. Является ли философия мировоззрением?
  4. В схеме, состоящей из конденсатора и катушки, происходят свободные электромагнитные колебания. Энергия конденсатора в произвольный момент времени t определяется выражением
  5. В этот момент все искажения пропали, появилась картинка лагеря демонов, но почему-то вверх ногами. Под нашими вопросительными взглядами Сергей занервничал.
  6. Вводите побуждающее происшествие основного сюжета как можно раньше... но не прежде, чем наступит подходящий момент.
  7. Векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.
  8. Вопрос 3. В какой момент включается специальная световая и звуковая сигнализация при следовании пожарного автомобиля к месту вызова?
  9. Вопрос 8 Момент инерции твердого тела
  10. Вот почему Лао-цзы так настаивает на том, что истина не может быть высказана, что в тот момент, когда вы высказали ее, вы ее фальсифицировали. Она уже не является истиной.
  11. ВРЕМЯ С МОМЕНТА ЗАПОМИНАНИЯ (в часах)
  12. Выборочные моменты

Уявно розiб’ємо АТТ на малi елементи об’ємом та масою m i якi можна вважати матерiальними точками (тобто представимо АТТ як систему матерiальних точок з масою m i).

Моментом iнерції І матерiальної точки вiдносно деякої осi z, називається добуток маси матерiальної точки mi на квадрат її вiдстанi , вiд цiєї осi (рис.2.5):

(2.28)

Момент iнерцiї всього тiла вiдносно деякоiї осi Z дорівнює сумi моментiв iнерції всiх його точок вiдносно цiєї осi:

(2.29)

Ця величина скалярна, одиниця вимiрювання в системi СІ — кг м2.

Момент iнерцiї має кожне тiло, незалежно вiд свого руху. Подiбно до того, як тiло має масу незалежно вiд свого стану руху чи спокою, воно має i момент iнерцiї вiдносно будь-якої осi незалежно вiд того, обертається воно навколо цiєї осi чи нi.

Як виходить iз означення (2.29), момент iнерцiї залежить не тiльки вiд маси тiла, але й вiд того, як ця маса розподiлена за об’ємом тiла. Враховуючи, що та переходячи вiд додавання до iнтегрування перепишемо вираз (2.29):

(2.30)

де ρ — густина речовини у вибраному об’ємi dV, r — вiдстань цього об’єму вiд осi, вiдносно якої обчислюється момент iнерцiї. Знаходження цього iнтеграла загалом випадках є досить складним. Задача значно спрощується, якщо розглядати однорiднi тiла правильної форми. Наведемо вирази для моментiв iнерцiї деяких таких тiл:

· момент iнерцiї диска (цилiндра) з радiусом R вiдносно осi симетрiї:

(2.31)

· момент iнерцiї обруча (тонкостiнного порожнього цилiндра) з радiусом R вiдносно осi симетрії:

(2.32)

· момент iнерції суцiльної кулi з радiусом R вiдносно осi, що проходить через центр кулi:

(2.33)

· момент iнерцiї однорiдного стрижня довжиною l вiдносно осi, що проходить через його середину перпендикулярну до l:

(2.34)

· те ж саме вiдносно осi, що проходить через кiнець стрижня:

(2.35)

Як бачимо, момент iнерцiї тiла залежить не тiльки вiд маси, форми i розмiрiв тiла, але й вiд розташування тiла вiдносно осi.

Можна обчислити момент iнерцiї тiла вiдносно будь-якої осi. Для цього зручно використовувати теорему Штейнера: момент iнерцiї тiла І вiдносно довiльноiї осi z ’дорiвнює сумi моменту інерції тiла I0, вiдносно осi, що проходить через його центр мас паралельно данiй осi z ’, i добутку маси тiла m на квадрат вiдстанi d мiж осями (рис. 2.6):

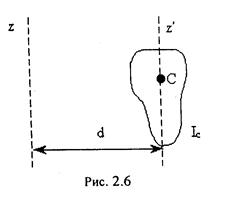
(2.36)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)