АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Неiнерцiальнi системи вiдлiку

Читайте также:
  1. I. Основні риси політичної системи України
  2. V. 2. Механічне описання молекулярної системи
  3. Автоматизовані системи управління процесом розформування составів на сортувальних гірках
  4. Адаптивні типи людини. Антропоекологічні системи і здоров'я.
  5. Аналіз роботи системи
  6. Англо-американський (прецедентний) тип правової системи
  7. Валютний ринок і валютні курси. Системи гнучких і фіксованих валютних курсів: порівняльна ефективність
  8. Взаємозв'язок ІС обліку з іншими підсистемами інформаційної системи підприємства.
  9. Визначення і складові грошової системи
  10. Вікно інтерфейсу системи
  11. ВІКОВІ ОСОБЛИВОСТІ ЕНДОКРИННОЇ СИСТЕМИ
  12. Внутрігосподарські системи розселення.

Досi ми розглядали рух в iнерцiальних системах вiдлiку. У таких системах, як вiдомо, виконується другий закон Ньютона, який можна записати у виглядi

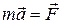(2.72)

Розглянемо тепер неiнерцiальнi системи вiдлiку, тобто такi, що рухаються прискорено вiдносно iнерцiальних систем.

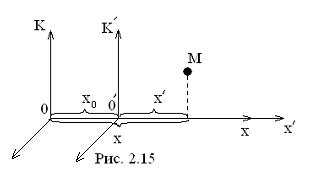
Нехай неiнерцiальна система К¢ рухається вздовж осi О х iнерцiальної системи К (рис. 2.15). Тодi для координати х ¢ точки М можна записати:

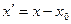(2.73)

 

 
 

Продиференцiюємо цей вираз двiчi за часом

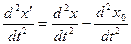, (2.74)

де 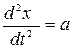- прискорення точки в системі К, - прискорення точки в системі К¢, 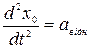- прискорення системи К відносно системи К¢.

Отже,

(2.75)

Помножимо лiву i праву частину цього виразу на масу точки m:

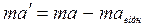
Бачимо, що в iнерцiальнiй системi в другому законi Ньютона крiм “звичайної” сили F з’явилася додаткова сила - 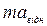. Назвемо її силою інерції 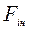. У векторному вигляді

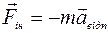, (2.76)

тобто сила iнерції напрямлена протилежно до прискорення неiнерцiальної системи вiдносно iнерцiальної.

Сили iнерцiї можна виміряти. Наприклад, прилади, що вимiрюють сили інерції, дають змогу з великою точнiстю визначати мiсце перебування лiтака чи ракети.

Оскільки сили iнерцiї зумовленi прискореним рухом неiнерцiальної системи вiдлiку, вони можуть проявлятися не тiльки при поступальному, але й при обертальному русi.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)