Кутове прискорення

Кутове прискорення характеризує змiну кутової швидкостi за часом. Аналогiчно до означень, наведених в п. 1.3.3, розрiзняють середнє i миттєве кутове прискорення.

Середнє кутове прискорення () визначається вiдношенням змiни кутової швидкостi до вiдповiдного промiжку часу:

(1.49)

Для миттєвого кутового прискорення (або просто кутового прискорення) можна записати:

(1.50)

Тобто воно чисельно дорiвнює першiй похiднiй кутової швидкості за часом або другiй похiднiй кута повороту за часом. Вимiрюється кутове прискорення в радiанах на секунду в квадратi (рад/с²). Воно також є псевдовектором, спрямованим по осi обертання

(1.51)

На рис.1.11, в напрямок вiдповiдає прискореному руху по колу, напрямок — сповiльненому руху по колу.

Знайдемо зв’язок мiж лiнiйними i кутовими характеристиками руху.

1. Зв’язок мiж лiнiйною i кутовою швидкiстю:

тобто

(1.52)

2. Зв’язок мiж тангенцiальним i кутовим прискоренням:

тобто

(1.53)

3. Зв’язок між нормальним прискоренням і кутовою швидкістю:

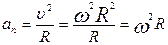
тобто

(1.54)

Для розв’язання оберненої задачi під час руху точки по колу використовують вирази аналогiчнi виразам (1.33) та (1.35):

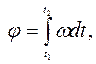(1.55)

(1. 56)

Тодi для рiвнозмiнного руху по колу вiдповiднi математичнi перетворення дадуть вирази аналогiчнi виразам (1.36), (1.37),(1.38):

(1.57)

(1.58)

(1.59)

де — початкова кутова швидкiсть у момент часу t =0, 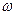— кутова швидкiсть у момент часу t.

Поиск по сайту: