Основне рiвняння релятивістської динамiки

Вiдповiдно до принципу вiдносностi Ейнштейна, всi закони природи повиннi бути iнварiантними вiдносно до iнерцiальних систем вiдлiку. Iншими словами, математичний запис законiв повинен мати однаковий вигляд в усiх цих системах.

Виявляється, що основне рiвняння динамiки Ньютона у виглядi не вiдповiдає цьому принципу. Разом з тим у теорiї вiдносностi доведено, що його задовольняє рівняння

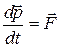, (4.13)

де 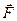— сила, що дiє на частинку. Наведене рiвняння за виглядом повнiстю збiгається з основним рiвнянням ньютонiвської динамiки (2.13), але фiзичний змiст рiвняння (4.13) iнший. У цьому рiвняннi злiва стоїть похiдна не вiд класичного, а вiд релятивiстського iмпульсу. Пiдставимо вираз (4.12) у рiвняння (4.13) i одержимо:

. (4.14)

Вираз (4.14) i є основним рiвнянням релятивістської динамiки. Вочевидь, що саме у такому виглядi рiвняння (4.14) приводить до збереження iмпульсу для вiльної частинки () i при υ -- с приймає форму основного рiвняння ньютонiвської динамiки (; де ).

З основного рiвняння релятивiстської динамiки (4.14) випливає несподiваний висновок: вектор прискорення 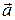частинки загалом випадку не збiгається за напрямком з вектором сили 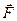. Дiйсно,

,

де — релятивiстська маса.

Продиференцiювавши цей вираз за часом, одержимо

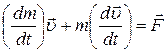(4.15)

Вираз (4.15) графiчно зображено на рис. 4.3, з якого видно, що вектор прискорення 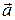не є колiнеарним вектору .

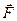Зазначимо, що вектор прискорення збігається за напрямком з вектором сили 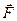тiльки у двох випадках: а) вектор сили 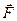перпендикулярний до вектора швидкостi 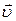(поперечна сила); б) вектор сили 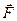паралельний вектору швидкостi 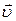(поздовжня сила). Оскiльки у першому випадку сила, що дiє на частинку — поперечна, то вона змiнює тiльки напрямок швидкостi й не змiнює саму величину швидкостi, тобто . За такої умови похiдна у виразi (4.15) дорiвнює нулю (релятивiстська маса m залежить вiд швидкостi, але в даному випадку , отже i ), i рiвняння (4.15) набуває вигляду

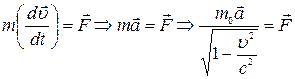
або

(4.16)

Вектори 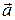i 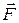збігається за напрямком.

У разі поздовжньої сили (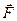 паралельна 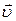) рiвняння (4.15) маємо право просто переписати у скалярному виглядi. Взявши похiднi у лiвiй частинi цього рiвняння, матимемо

,

звідки

або у векторному вигляді

(4.17)

З виразiв (4.16) i (4.17) бачимо, що за однакових в обох випадках значеннях сили F i швидкостi υ поперечна сила надає частинцi бiльшого прискорення, нiж поздовжня сила.

Поиск по сайту: