Кiнетична енергiя релятивiстської частинки

Визначимо кiнетичну енергiю так, як i у класичнiй механiцi, а саме, як величину, прирощення якої дорiвнює роботi сили, що дiє на частинку.

(4.18)

Згiдно з рiвнянням (4.13)

,

де m — релятивiстська маса. Отже, враховуючи, що , a

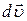де — проекцiя вектора на напрямок вектора (ця проекція дорiвнює — прирощенню модуля вектора швидкостi, тому () маємо

(4.19)

Пiднесемо формулу (4.11) до квадрата i перетворимо її до вигляду

(4.20)

Тепер знайдемо диференцiал цього виразу, маючи на увазi, що і c - постiйнi величини:

Подiливши вираз (4.21) на 2 m, одержимо

c²dm=υ²dm+mυdυ (4.22)

Права частина виразу (4.22) збiгається з правою частиною виразу для кiнетичної енергiї (4.19).

Тож маємо записати

(4.23)

Таким чином, прирощення кiнетичної енергiї частинки пропорцiйне прирощенню її релятивiстської маси. Кiнетична енергiя нерухомої частинки дорiвнює нулю, а її маса дорiвнює . Отже, проiнтегрувавши вираз (4.23), маємо

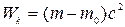(4.24)

або

(4.25)

Це i є вираз для релятивiстської кiнетичної енергії. Якщо υ «с, то має бути вираз для класичної кiнетичної енергії . Скористаємося формулою бiнома Ньютона, відповідно до якої

За умови υ «с можна обмежитися тiльки двома членами ряду i тодi вираз (4.25) перетвориться на

(4.26)

Таким чином, при υ «с вираз для релятивiстської кiнетичної енергiї (4.25) перетворюється на класичний вираз для кiнетичної енергії. Зазначимо, що аналогiчно до класичної механiки релятивiстську кiнетичну енергiю не можна подати у виглядi , де — релятивiстська маса частинки.

Поиск по сайту: