Реактивний рух

Рух деяких тiл супроводжується змiною їх маси. Наприклад, маса ракети зменшується за рахунок витоку газiв, що утворюються при згораннi палива. При вильотi їх в одному напрямку, ракета отримує iмпульс у протилежному напрямку. У цьому полягає фiзичиий змiст реактивного руку, який використовується в рiзноманiтних лiтаючих апаратах.

Виведемо рiвняння руху ракети як тiла змiнної маси. Розглянемо систему ракета з газами. Нехай у певний момент часу t маса ракети разом iз газами m, а її швидкiсть вiдносно землi υ. Вiдповідно iмпульс ракети дорiвнює .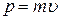

За час dt з ракети вилетiли гази масою dm iз швидкiстю u вiд ракети (цю швидкiсть часто називають швидкiстю газової струмини). У результатi цього маса ракети зменшилася на dm i почала дорiвнювати m-dm, а швидкiсть υ збiльшилася на dm i стала дорівнювати u-u вiдносно Землi. Вiдповiдно iмпульс ракети буде дорівнювати, а iмпульс газiв, що вилетiли дорiвнюватиме . Звертаємо увагу, що гази летять у протилежний бiк ракети, тому перед u ставимо знак “-„. Запишемо тепер змiну iмпульсу всiєї системи ракета-гази, що вилетiли за час ‚ dt:

або

(3.7)

Розкривши дужки будемо мати:

(3.8)

Проаналiзуємо цей вираз у разі, коли зовнiшнi сили дiють на ракету випадок (а) i не дiють на ракету випадок (б) (пiд зовнішніми силами розумiють гравiтацiйнi сили притягання Сонця, Землi, планет, сили опору повiтря та ін.:

а) нехай на ракету дiють зовнiшнi сили. Позначимо їх рiвнодiйну F. Тодi за другим законом Ньютона

, (3.9)

або підставивши dp, маємо:

, (3.10)

Подiливши цей вираз на dt ‚ матимемо:

. (3.11)

Цей вираз називається рiвнянням Мещерського. Звернемо увагу, на те, що в рiвняннi Мещерського до зовнiшньої сили F додається векторна величина . Вона характеризує механiчну дiю на ракету частинок газу, що відділяються вiд неї, i називається реактивною силою:

(3.12)

Як бачимо, реактивна сила пропорцiйна добутку маси газiв, що вiддiляються за одиницю часу, i швидкостi газової струмини. Ця залежнiсть є основою для розрахунку сили тяги реактивних двигунiв всiх систем;

б) якщо на ракету зовнiшнi сили не дiють (полiт у космiчному просторi на великiй вiдстанi вiд планет), то за законом збереження iмпульсу , тодi вираз (3.8) буде:

(3.13)

Це означає, що ракета рухається тiльки пiд дiєю реактивноiї сили. Визначимо, яку максимальну швидкiсть метиме при цьому ракета. Нехай початкова швидкiсть ракети дорiвнює нулю, її траєкторiя — пряма лiнiя, а гази вилiтають iз сталою швидкiстю u. Це означає, що вектори υ і u протилежно спрямованi. Тому можна записати в скалярному виглядi:

. (3.14)

Нехай початкова маса ракети , її кiнцева маса пiсля повного вигоряння палива масою буде ( — ). Тодi максимальна швидкiсть ракети при змiнi її маси вiд до — може бути знайдена шляхом iнтегрування виразу (3.14):

(3.15)

Вираз

(3.16)

називається формулою Цiолковського. За цiєю формулою можна розрахувати запас палива, необхiдний для надання ракетi певної швидкостi υ. Бачимо, що чим бiльша швидкiсть газової струмини и, тим бiльшою може бути корисна маса ракети ( — ).

Удар

Взаємодiя мiж тiлами називається ударом, якщо:

— вiдбувається за дуже короткий час;

— внутрiшнi сили взаємодiї настiльки великi, що зовнiшнiми силами можна знехтувати i розглядати тiла, що спiвударяються, як замкнену систему.

Введемо такi умови

• тiла до i пiсля удару рухаються вздовж прямої, що проходить через їх центр мас, тобто удар є центральним;

• тiла рухаються поступально (не обертаючись);

• сили тертя не враховуються.

Розглянемо два граничних випадки центрального удару — абсолютно пружний i абсолютно непружний удар.

1. Абсолютно пружним називається удар, за якою механiчна енергiя тiл, що спiвударних, зберiгається. Це означає, що та частина кiнетичної енергiї, що пiд час удару перейшла в потенціальну енергiю пружної деформацiї, пiсля цього знову перетворюється на рiвну їй кінетичну енергiю. Тому при абсолютно пружному ударi виконуються два закони: збереження механiчної енергiї та збереження iмпульсу.

Нехай два абсолютно пружних тiла з масами i рухаються вздовж осi х зi швидкостями відповідно та (рис.3.1,а). Пiсля абсолютно пружного удару вони набувають швидкостей вiдповідно та (рис.3.1,б).

Запишемо закон збереження механiчної (а саме кiнетичної) енергії та закон збереження iмпульсу для цього випадку:

Розв’язок цiєї системи рiвнянь дає такі вирази для швидкостей тiл пiсля удару:

Проаналiзуємо цi вирази для окремо взятих випадкiв:

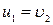а). Маси тiл однаковi ( = = ), тодi i тобто при ударi тiла обмiнюються швидкостями. Якщо ж до удару одне тiло було нерухомим, то пiсля удару нерухомим буде друге тiло;

б). Маса одного тiла значно бiльша за масу другого тiла (наприклад ; ). Тодi i . Тобто швидкість масивного тiла практично не змiнюється.

Коли ж масивне тiло було нерухомим (наприклад, стiна), то 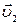=0 i = , тобто тiло, що рухається, вiдскакує в протилежний бiк з такою ж швидкiстю.

2. Абсолютно непружним ударом називається зiткнення двох тiл, в внаслідок чого тiла об’єднуються i рухаються далi разом. Зрозумiло, що в цьому разі закон збереження механiчної енергiї не виконується (кiнетична енергiя частково витрачається на деформацiю), а закон збереження iмпульсу — виконується.

Нехай до удару швидкостi тiл з масами 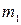i були вiдповiдно і 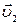а після удару обидва тіла почали рухатися разом зі швидкiстю (рис. 3.2б)

Запишемо закон збереження iмпульсу:

(3.21)

Звiдси швидкiсть тiл пiсля удару дорівнює:

(3.22)

Тобто, якщо тiла рухалися назустрiч одне одному, то пiсля удару вони будуть рухатимуться в бiк, руху тiла, яке мало бiльший iмпульс.

Поиск по сайту: