Робота, потужнiсть, коефiцiєнт корисної дії

Робота

Розглянемо матерiальну точку, що рухається довiльною траєкторiєю L пiд дiєю змiнної сили 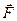(рис. 2.10).

Розiб’ємо цю траєкторiю на елементарнi перемiщення 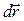так, щоб на кожному такому перемiщеннi дiючу силу можна було б вважати постiйною.

Тодi скалярний добуток сили 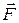на перемiщення буде називатись елементарною роботою :

, (2.46)

або

(2.47)

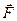де — кут мiж векторами i .

Оскiльки ,тобто є проекцiєю сили 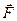на дотичну 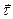до траєкторiї в даному мiсцi, то вираз (2.47) можна записати як

(2.48)

При 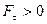, тобто кут гострий, то 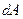; 0. Вiдповiдну силу часто називають рушійною силою (наприклад, сила тяги лiтака або ракети).

При 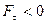, тобто коли кут тупий, 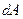-0 i вiдповiдно силу називають гальмуючою силою (наприклад, сила тертя чи опору).

Якщо ж кут = то 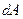= 0 i вiдповiдна сила роботи не виконує (наприклад, сила тяжiння при горизонтальному русi потягу або доцентрова сила).

Повна робота сили (F) при перемiщеннi з точки 1 в точку 2 буде визначатися сумою елементарних робiт, для обчислення якої слід проiнтегрувати вираз (2.47) або (2.48):

(2.49)

Якщо тiло рухається прямолiнiйно пiд дiєю постiйної сили (тобто F = соnst, соs = соnst), то в цьому частинному випадку, враховуючи, що dr = dS, з виразу (2.49) отримуємо:

тобто

(2.50)

Одиницею роботи в системi СІ є джоуль (Дж). 1Дж=1Н×м. Роботу сили можна знайти графiчно, якщо відомо її залежнiсть вiд перемiщення (рис.2.11). Добуток на , (див. рис. 2.11), що визначає елементарну роботу , є площиною прямокутника з основою i висотою . Тодi повна робота, як сума таких прямокутникiв, чисельно дорiвнює всiй площi заштрихованої криволiнiйної трапеції, тобто площi пiд графiком функцiї . Такий пiдхiд часто математично спрощує обчислення роботи.

Для прикладу знайдемо роботу зовнiшньої сили, що розтягує пружину (рис.2.12,а). За третiм законом Ньютона ця сила дорiвнює силi пружностi = , але протилежна їй за напрямком: , тому

(2.51)

Графiк цiєї сили подано на рис. (2.12,б). Робота зовнiшньої сили є додатною i чисельно дорiвнює площi заштрихованого трикутника

Цей же вираз можна одержати з виразу (2.49), пiдставивши вираз (2.51):

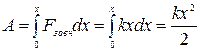(2.52)

Розглянемо роботу у разi обертального руху. Нехай до АТТ прикладено дотичну силу , пiд дiєю якої воно повернулося на малий кут (рис. 2.13). При цьому точка прикладання сили перемiстилася на 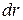. Як вiдомо, переміщення 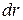можна визначити через радiус R та кут : 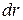R . Як видно з рис. 2.13, R = l, де l — плече сили . Тодi вiдповiдно до виразу (2.48.) елементарна робота дорiвнюватиме:

Оскільки F_tl=M, то

(2.53)

тобто елементарна робота при поворотi тiла на елементарний кут чисельно дорiвнює добутку моменту дiючої сили на цей кут. Якщо ж тiло повернулося на певний кут вiд положення до положення , то повну роботу в обертальному русi знайдемо шляхом iнтегрування виразу (2.53):

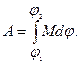(2.54)

Зокрема, коли момент дiючої сили є постiйною величиною (М =соnst) з виразу (2.54) маємо, що

(2.55)

Поиск по сайту: