 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Прискорення
|
Читайте также: |
Прискоренням називається фiзична величина, що характеризує змiну швидкостi з часом. Розрiзняють прискорення середнє i миттєве.
Середнє прискорення (
)— це векторна величина, що визначається вiдношенням змiни швидкостi 
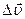до промiжку часу 
, за який ця змiна вiдбулася:
(1.16)
Напрямок вектора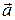 
збігається з напрямком .
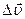Миттєве прискорення (або просто прискорення) 
, тобто прискорення в певний момент часу це границя, до якої прямує середнє прискорення при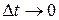 
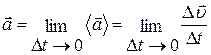(1.17)
Використовуючи рівність (1.16) маємо,
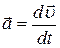(1.18)
Прискорення є векторна величина, що дорівнює похiднiй вектора швидкості за часом. З урахуванням формули (1.16) прискорення можна записати як другу похiдну радіус-вектора за часом:
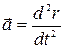(1.19)
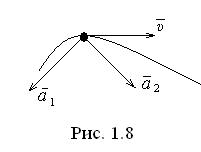Як буде показано далi, в загалом вектор 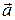спрямований пiд кутом до вектора 
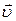в бiк угнутостi траєкторiї. На рис. 1.8. вектор 
вiдповідає прискореному руху, вектор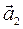 
—сповiльненому руху. Оскiльки змiна швидкостi вiдбувається i за модулем i за на напрямком, розрiзняють двi складовi прискорення:
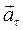- прискорення (дотичне), яке характеризує змiну швидкості за модулем i спрямоване по дотичнiй до траєкторії;
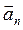- нормальне прискорення (доцентрове), яке характеризує змiну швидкості за напрямком i спрямоване по нормалi до траєкторії.
Повне прискорення дорівнює їх векторнiй сумi
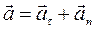(1.20)
Для знаходження цих складових прискорення, пiдставимо вираз для швидкостi в означення (1.18) i зробимо вiдповiдне диференцiювання:
Враховуючи, що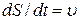 
, а 
можна подати у виглядi:
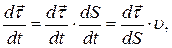
Матимемо вираз:
(1.21)
Можна показати, що
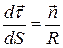, (1.22)
де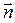 
- орт нормалі, R – радіус кривизни траєкторії в даній точці.
Остаточно вираз (1.21) набуде вигляду:
(1.23)
Порiвнюючи цей вираз з рiвнянням (1.20) бачимо, що перший член виразу визначає тангенцiальне прискорення
(1.24)
що спрямоване по дотичнiй до траєкторiї в данiй точцi i за модулем дорівнює
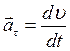. (1.25)
Другий член визначає нормальне прискорення
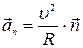, (1.26)
що спрямоване по нормалi до траєкторії в данiй точцi (тобто до центру кривизни траєкторiї) i за модулем дорівнює
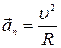(1.27)
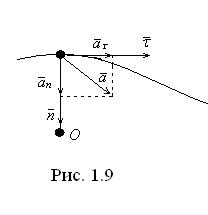
Як видно з рис.1.9, модуль повного прискорення
(1.28)
Аналогiчно до того, як записувався вектор швидкостi, вектор прискорення теж можна подати через проекцiї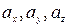 
на координатнi осi:
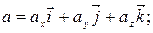(1.29)
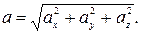(1.30)
Цi проекцiї знаходяться як похiднi за часом:
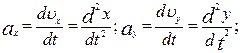
(1.31)
Поиск по сайту: